3D Drawings with Hidden Surface Removal
Introduction
It is important to be able to depict 3 dimensional objects in order to fully describe solid objects and especially the motion of solid objects. The following will document some basic concepts for doing that.
Vectors
A vector has both a direction and a length. Its mathematical description is:
![]() (1)
(1)
where (x,y,z) are the lengths (Cartesian components) of the vector components along the bold (x,y,z) unit vectors which have the ^ above them to denote that they are unit vectors.
Vector Rotations
A vector may be rotated by multiplying it by a rotation matrix. For example if we want to rotate the vector in equation 1 about the z axis by an angle fz we apply the following matrix:
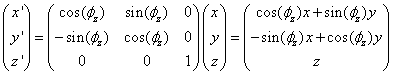 (2)
(2)
In the above case, for simplicity assume that y=0 and 0<fz <p/2. Then we will have a
positive x component and a negative y component which would seem to result in a
clockwise rotation about the z axis.
However, the standard z axis is defined by the direction that a
clockwise-threaded screw moves when rotated from x to y directions and that is
outward away from the x-y plane. So,
relative an observer looking along the positive z axis, the above rotation is a
counter-clockwise one.
Describing Polygons Using Vectors.
The simplest polygons are triangles and rectangles. To define one of them in 3 dimensional space we need 3 or 4 vectors. However, if we are referring to a continuous surface where the polygons are adjacent to one another, we need many less vectors for each polygon. As an example, take the case where we have a surface made up of squares where there are n squares in the horizontal direction and m squares in the vertical direction. The total number of squares is obviously the product n*m but the total number of vectors needed for this are (n+1)*(m+1) where 1 is added to each multiplicand in order to provide right and bottom edges of the rectangle.
While the vectors described above are all that are necessary for describing the polygons, it is programmatically simpler to provide all three or four vectors for each simple polygon.
Projecting the vectors onto the screen
Once the vectors for each polygon are formed, it is necessary to project them onto the 2-dimensional screen. To do that, we just eliminate one (say, the x) component of the vector.
Hidden surface removal
We would like to eliminate the (back) polygons that should be behind the front polygons. If we have done our projection by eliminating the x component of the vectors, then the ones that need to be eliminated are the ones whose outward normal vector’s x components are negative. This, of course, assumes that the positive x direction is out of the screen. For either a rectangular or triangular polygon, the outward normal vector is described by the cross-product:
![]()
where vectors r1, r2, r3 (see Figure 1) sequentially define the polygon vertices in a counter-clockwise direction as viewed from the “outside”.
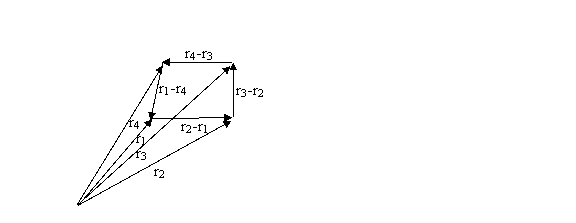
Figure 1: A polygon
whose vertices are defined by vectors r1, r2, r3
and r4. The sides of the
polygon are (r2-r1), (r3-r2), (r4-r3),
and (r1-r4).