Aircraft Moments and Rotation

Introduction

            An aircraft is an example of a somewhat symmetrical object that has three principal axes of rotation, pitch, roll, and yaw.  Since the wings and fuselage masses usually lie in almost the same plane, it can be modeled with reasonable accuracy as a planar object.  The advantage of doing this is that the yaw moment becomes a simple sum of the pitch and roll moments and all three axes of rotation pass through the center of mass (CM) which usually lies at about 30% of the wing chord behind the wing leading edge. A simplified diagram of the masses and CM location is shown below.

Figures

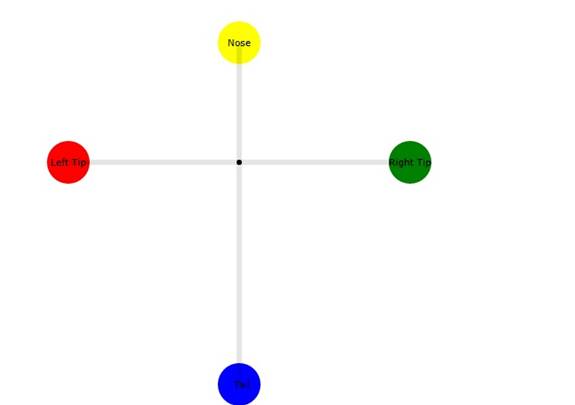
Figure 1: Showing the aircraft modeled as 4 spherical masses.  The wingtips, nose, and tail are labeled.  The black dot is the center of mass, so the tail sphere has to have less mass than the nose sphere.

Moments of Inertia

            These will be labeled IP, IR, and IY where the subscripts stand for pitch, yaw, and roll, respectively.  To define them we first need to compute the nose and tail masses from the center of mass location.  If the CM is located at a fraction Cg from the nose, then the ratio of the nose to tail mass is:

m N m T = 1− C g C g MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaamaalaaabaGaam yBamaaBaaaleaacaWGobaabeaaaOqaaiaad2gadaWgaaWcbaGaamiv aaqabaaaaOGaeyypa0ZaaSaaaeaacaaIXaGaeyOeI0Iaam4qamaaBa aaleaacaWGNbaabeaaaOqaaiaadoeadaWgaaWcbaGaam4zaaqabaaa aaaa@407F@  

(1.1)

If the sum of the nose and tail masses (fuselage mass) is Mf then the nose and tail masses are:

m N = M F (1− C g ) m T = M F C g MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOabaeqabaGaamyBam aaBaaaleaacaWGobaabeaakiabg2da9iaad2eadaWgaaWcbaGaamOr aaqabaGccaGGOaGaaGymaiabgkHiTiaadoeadaWgaaWcbaGaam4zaa qabaGccaGGPaaabaGaamyBamaaBaaaleaacaWGubaabeaakiabg2da 9iaad2eadaWgaaWcbaGaamOraaqabaGccaWGdbWaaSbaaSqaaiaadE gaaeqaaaaaaa@466B@  

(1.2)

Since all the nose and tail weights are concentrated in two small spheres, the pitch moment of inertia about the CM is:

I P = m N l f 2 C g 2 + m T l f 2 (1− C g ) 2 = M F l f 2 (1− C g ) C g 2 + M F l f 2 (1− C g ) 2 C g = M F l f 2 [ C g (1− C g )][ C g +(1− C g ]= M F l f 2 [ C g (1− C g )] MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOabaeqabaGaamysam aaBaaaleaacaWGqbaabeaakiabg2da9iaad2gadaWgaaWcbaGaamOt aaqabaGccaWGSbWaa0baaSqaaiaadAgaaeaacaaIYaaaaOGaam4qam aaDaaaleaacaWGNbaabaGaaGOmaaaakiabgUcaRiaad2gadaWgaaWc baGaamivaaqabaGccaWGSbWaa0baaSqaaiaadAgaaeaacaaIYaaaaO GaaiikaiaaigdacqGHsislcaWGdbWaaSbaaSqaaiaadEgaaeqaaOGa aiykamaaCaaaleqabaGaaGOmaaaakiabg2da9iaad2eadaWgaaWcba GaamOraaqabaGccaWGSbWaa0baaSqaaiaadAgaaeaacaaIYaaaaOGa aiikaiaaigdacqGHsislcaWGdbWaaSbaaSqaaiaadEgaaeqaaOGaai ykaiaadoeadaqhaaWcbaGaam4zaaqaaiaaikdaaaGccqGHRaWkcaWG nbWaaSbaaSqaaiaadAeaaeqaaOGaamiBamaaDaaaleaacaWGMbaaba GaaGOmaaaakiaacIcacaaIXaGaeyOeI0Iaam4qamaaBaaaleaacaWG NbaabeaakiaacMcadaahaaWcbeqaaiaaikdaaaGccaWGdbWaa0baaS qaaiaadEgaaeaaaaGccqGH9aqpaeaacaWGnbWaaSbaaSqaaiaadAea aeqaaOGaamiBamaaDaaaleaacaWGMbaabaGaaGOmaaaakiaacUfaca WGdbWaaSbaaSqaaiaadEgaaeqaaOGaaiikaiaaigdacqGHsislcaWG dbWaaSbaaSqaaiaadEgaaeqaaOGaaiykaiaac2facaGGBbGaai4qam aaBaaaleaacaWGNbaabeaakiabgUcaRiaacIcacaaIXaGaeyOeI0Ia am4qamaaBaaaleaacaWGNbaabeaakiaac2facqGH9aqpcaWGnbWaaS baaSqaaiaadAeaaeqaaOGaamiBamaaDaaaleaacaWGMbaabaGaaGOm aaaakiaacUfacaWGdbWaaSbaaSqaaiaadEgaaeqaaOGaaiikaiaaig dacqGHsislcaWGdbWaaSbaaSqaaiaadEgaaeqaaOGaaiykaiaac2fa aaaa@8B9C@  

(1.3)

where the fuselage length is lf. The above equation makes sense since for Cg=1/2, and lf =2l, then we would have I=Mfl2 as expected for small masses located at distance l from the CM. 

The roll moment of inertia is:

I R = M W 2 ( l w 2 ) 2 MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadMeadaWgaa WcbaGaamOuaaqabaGccqGH9aqpdaWcaaqaaiaad2eadaWgaaWcbaGa am4vaaqabaaakeaacaaIYaaaamaabmaabaWaaSaaaeaacaWGSbWaa0 baaSqaaiaadEhaaeaaaaaakeaacaaIYaaaaaGaayjkaiaawMcaamaa CaaaleqabaGaaGOmaaaaaaa@40DE@  

(1.4)

where Mw is the total mass of the wings and lw is the wingspan.

Since we have a planar object, the yaw moment of inertia is just the sum of the pitch and roll moments:

I Y = I P + I R MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadMeadaWgaa WcbaGaamywaaqabaGccqGH9aqpcaWGjbWaaSbaaSqaaiaadcfaaeqa aOGaey4kaSIaamysamaaBaaaleaacaWGsbaabeaaaaa@3D5F@  

(1.5)