Balloon Bouncing in Vacuum

Introduction

Everybody knows that balls successively bounce less and less high after they're dropped. The change in height is due to a catchphrase called the "coefficient of restitution" (CR) which is less than 1. The CR is due to the compressive heating of the ball material. For a solid ball this compressive heating is very complicated to model but for an gas-filled ball with very thin walls an accurate animation model is possible. That model is the goal of this animation.

Realization

Since the ball must be very thin walled we will call it a balloon where the mass of the walls is much less than the mass of the gas inside. A typical gas at standard pressure and temperature (STP) has a mass of about 1 gram per liter or 1 kilogram per cubic meter (Recall that 1 gram molecular weight of any gas at STP displaces 22.4 liters). So for a fairly large diameter balloon it is reasonable that the gas inside have more mass than the walls of the balloon. Further, since the mass of the balloon won't much exceed the mass of the gas that it displaces, as well as for other reasons like air drag, we will assume that the balloon bounces in vacuum. We will also assume that the distortion of the balloon walls during impact does not result in the walls absorbing significant energy.

Figures

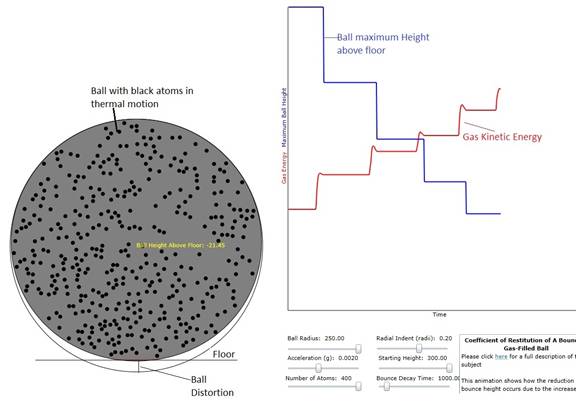
Figure 1: Illustration of the animation. The ball with the gas inside it is shown in the colliding position. Note that the height above the floor is updated in real time in the color yellow. The maximum bounce height (blue) and the gas kinetic energy are also plotted.

Math-Energy

The total initial energy of the balloon is the energy of the gas atoms inside as well as the gravitational energy due to its center of mass height, h, above the floor from which it bounces.

$E_{0} = E_{k 0} + M g h_{0}$

where E_k is the total kinetic energy of the gas atoms and, M is their total mass, and g is the acceleration of gravity.

When the ball hits the floor the first time the kinetic energy of the gas atoms will increase because of compression and therefore, since total energy is conserved, the height to which the ball bounces will be reduced.

$E_{1} = E_{0} = E_{k 1} + M g h_{1}$

Solving for both h₀ and h₁ we obtain:

$h_{0} = \frac{E_{0} - E_{k 0}}{M g}$

$h_{1} = \frac{E_{0} - E_{k 1}}{M g}$

More importantly, the change in h is given by:

$δ h = \frac{- (E_{k 1} - E_{k 0})}{M g} = \frac{- δ E_{k}}{M g}$

where we recall that δE_k will be a positive number.

Math-Collision with Floor

We will choose to model the indentation of the balloon by using a sinusoid.

$r (t) = r_{0} - d \sin [ω (t - t_{c})]$

where d is the maximum indentation, ω is to be computed and t_c is the time of the collision. The speed of the original center of the balloon at the moment of collision will be designated v_c and the initial speed of indentation must match v_c.

${\frac{d r}{d t})}_{t = t_{c}} = ω d = v_{c}$

where from the previous section:

$v_{c} = \sqrt{2 g h_{0}}$

which allows us to compute ω.

After the initial impact, the balloon will remain in contact with the floor for a time t_f. That would mean that the original center of the balloon will continue to move first downward and then upward at some computed rate to match the indentation and recovery of the indentation. In order to stay in contact the downward speed of the original center of the balloon's y position must follow the time dependence:

$v_{y} (t) = v_{c} \cos [ω (t - t_{c})]$

In order to take into account the fact that the kinetic energy associated with the balloon's movement will be reduced on the upward leg of its journey, we will modify the above equation with an exponential rolloff of v_c.

$v_{y} (t) = v_{c} \exp (- \frac{t - t_{c}}{τ_{E}}) \cos [ω (t - t_{c})]$

where τ_Eis some time constant that must be computed from the internal energy gain of the gas.

The recovery of the balloon will stop at

$ω (t_{s} - t_{c}) = π$

where t_s is the stopping time at which time the original center of the balloon will have speed:

$v_{y} (t_{s}) = - v_{c} \exp (- \frac{π}{ω τ_{E}})$

For a 10% loss of speed, the value of t_Ewould then be:

$\begin{array}{l} \exp (- \frac{π}{ω τ_{E}}) = \frac{v}{v_{c}} = 0.9 \\ \frac{π}{ω τ_{E}} = - \ln (0.9) \\ ω τ_{E} = - \frac{π}{\ln (0.9)} \end{array}$

Since the kinetic energy is proportional to the square of v_y(t_s), the change in maximum ball height will be

$m g δ h = \frac{1}{2} m (v {(t_{s})}^{2} - v_{c}^{2})$

where, obviously, δh will be a negative number.

In fact we won't have information about the speed (or energy) loss until the ball has finished its indentation and recovery. So we'll need to compute the value of τ_E from previous test experiments.