Liquid Barometer

Introduction

            A barometer consists of a liquid-filled tube or tube that has its open end in a larger vat of the liquid.  The tube is first filled with the liquid by inverting it and pouring the liquid in until it is full.  Then, with the open end stoppered, that end is inserted into the vat and the tube is stood upright with the closed end upward. Then the stopper in the lower end is removed so that some of the tube's liquid flows back into the vat, leaving a good vacuum at the closed end.  The liquid should have a low vapor pressure at all temperatures under which the barometer will be used.  Also, for compactness, the liquid density will usually be high. For earth's sea level ambient pressure mercury is a good choice and with its density of 13.53 resulting in a column height of just 760 mm.  Please read the caption on Figure 1.

 

 

 

 

 

 

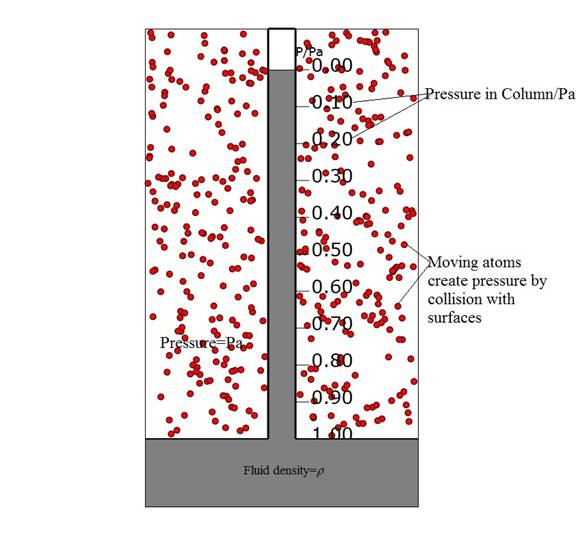
Figure 1: Components of a liquid barometer. The tube is the narrow vertical column with the short vacuum at the top.  The tube is standing in a vat of the liquid with its lower end open.  The collisions of the moving atoms with the surface of the vat liquid results in force on that surface and an internal hydrostatic pressure.  That pressure exists also in the liquid column but is linearly reduced as a function of the height in the tube, as shown by the scale to its right.

 

Physics

            The pressure due to the bombardment of the surface of the fluid by air at STP is about 100,000 Pascals  (newtons m-2 ).  In earth's gravity the downward force due to a column of liquid (mercury here) of cross section area A and height h is

F=ρghA MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadAeacqGH9a qpcqaHbpGCcaWGNbGaamiAaiaadgeaaaa@3C1B@  

(1.1)

where ρ is the density of mercury (13.53 grams cm-3 or 13,530 kg m-3) and g is the acceleration of gravity 9.81 m sec-2.  For a mercury  column that is one meter high and has a cross sectional area of one square meter then the force is 131,000 Newtons.   Then the height of a mercury column supported by air pressure is just this result scaled to 100,000 newtons.

 

           

h STP = F ρgA = 100,000 133,000 =0.753 m MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadIgadaWgaa WcbaGaam4uaiaadsfacaWGqbaabeaakiabg2da9maalaaabaGaamOr aaqaaiabeg8aYjaadEgacaWGbbaaaiabg2da9maalaaabaGaaGymai aaicdacaaIWaGaaiilaiaaicdacaaIWaGaaGimaaqaaiaaigdacaaI ZaGaaG4maiaacYcacaaIWaGaaGimaiaaicdaaaGaeyypa0JaaGimai aac6cacaaI3aGaaGynaiaaiodacaaMc8UaaiyBaaaa@5148@

(1.2)

or 753 mm where the standard barometer reading at STP is 760 mm.

 

Discussion

            A common problem with using atmospheric pressure as the scaling for a barometer is that 100,000 newtons is also the weight of a column of air with a 1meter2 cross-section reaching from the earth's surface to outer space, with, of course decreasing density as altitude increases.  This weight concept is not required for the barometer to work.  In fact, we could have the rectangular area (box) shown in Figure 1 in vacuum and then connect a pump to provide gas (or air) pressure to the box and the barometer would function exactly the same as with atmospheric pressure.  In fact that is what we'd have to do to provide the variations shown by the sliders in the animation.  To provide the variation in average atom energy we'd need to heat the gas going in to the box and to provide the variation due to atomic number density we'd need to compress the gas.