Bernoulli Principle
Introduction
This will document an animation of the Bernoulli effect for a gas of atoms at a finite temperature. The gas will have both the random motion due to its temperature and a variable drift speed along the x axis as it passes through a constriction called a venturi. Venturis have been used in carburetors of internal combustions engines for at least 90 years. Their function was to provide a region of reduced pressure that could pull fuel up out of the carburetor bowl and vaporize it making it ready for combustion inside the engine. In this animation it is assumed that the density of the atoms remains almost constant so that the atoms must speed up as the walls of the venturi get closer together. It is also assumed that the temperature of the gas doesn't significantly change. Since it can only be the change of pressure that causes the increase of speed, the law of conservation of energy require that the pressure be lower at the midpoint of the venturi than at the entrance.
Figures
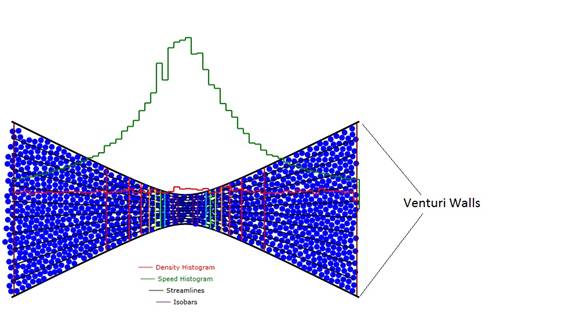
Figure 1: Showing the venturi walls (black), molecules
(blue), density histogram (red), and speed histogram (green), streamlines
(black,)and lines of constant pressure (isobars, spectrally colored violet at
the lowest pressure and deep red at the highest pressure)). Note that the
product of the venturi channel width times the speed is approximately constant
as it must be to keep the density constant.
Calculations
In a two dimensional channel (venturi) with a flow of incompressible particles or molecules through it, the longitudinal drift speed of the atoms is inversely proportional to the spacing, w, between the two walls of the channel.
![]() (1)
(1)
where w0 is the spacing at the entrance and exit of the venturi and w(x) is the spacing at position x.
I have chosen to define the walls of the channel by two hyperbolas:
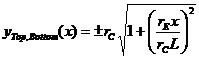 (2)
(2)
where rC is the half width of the channel at its center, rE is the half width of the channel at its entrance and exit, (x,y)=(0,0) is the symmetry point of the channel, and L is the half length of the channel.
If the flow is to be incompressible then the velocity (vx,vy) has to be derivable from a potential. For our case, that potential will be:
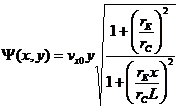 (3)
(3)
where (vx0,0) is the velocity far away from the channel. It will turn out that the velocities are
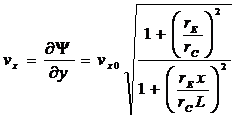 (4)
(4)
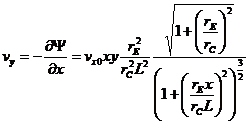 (5)
(5)
Note that if y follows the contours of equation 2, the potential values on the channel walls will be:
![]() (6)
(6)
which is a constant so that the walls are constant potential surfaces.
The partial differential equation governing the flow of particles is the equation of continuity:
![]() (7)
(7)
where n is the particle density (particles m-2) and t is time. Since we have declared that these particles are incompressible, we must have
![]()
and therefore:
![]() (8)
(8)
Using equations 4 and 5 in equation 8 we get:
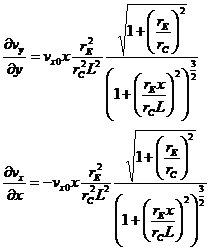 (9)
(9)
so that equation 8 is satisfied.
More generally, we note that since
![]() (10)
(10)
![]()
![]()
for any continuous function of x and y.
Boundary Collisions
For wall collisions we will make the assumption that, with respect to the normal of the boundary, the exiting velocity angle is the same as the incoming velocity. It will be seen that this does not change the energy of the particle. The inward (pointing toward the inside of the channel) unit normal vector to the boundary at point x is defined in terms of the slope, y'(x)=dy/dx, of the boundary at point x.
![]() (11)
(11)
where the B,T subscripts on vector n refer to bottom and top boundaries, respectively, and x and y with carats over them are unit vectors along the x and y
directions.
The unit vectors tangential to the top and bottom boundaries can be described by
![]() (12)
(12)
where we note that t is orthogonal to n since their dot product is:
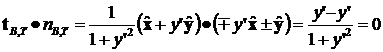 (13)
(13)
The velocity vector incident on the boundaries can be described by its components along the normal and tangential vectors as:
![]() (14)
(14)
which can more conveniently written as the matrix expression:
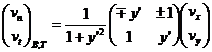 (15)
(15)
Our collision results in negation of the normal component of the incoming velocity while the tangential component stays the same. Thus:
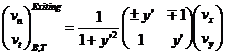 (16)
(16)
This result must be converted to the x and y components of v. To
do that we just both sides of equation 15 by the inverse of the matrix in
equation 15
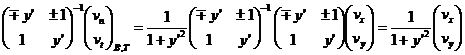
so that:
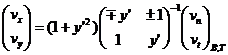 (17)
(17)
Inserting the expression 16 for the exiting velocity into equation 17 we obtain:
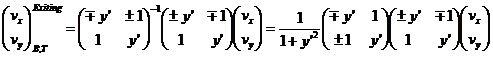
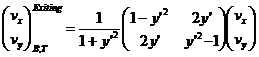 (18)
(18)
Particle-Particle Collisions
Here we will consider spherical particles all of which have the same mass, m, and diameter, D. The centers of the spheres will be labeled (x1,y1) and (x2,y2). Upon collision, the momentum transferred between the spheres will always be along the unit vector:
![]() (19)
(19)
where
![]()
is the distance between centers.
Since the masses are the same, the expression for the final velocities in terms of the initial velocities is:
![]() (20)
(20)
where the apostrophe on the left side of the equations indicates the final velocities. We know that the energies are conserved so
![]() (21)
(21)
The directions of the change in velocities are along the vector of centers, u, and the values of the changes of velocities must be equal and opposite.
![]() (22)
(22)
so that
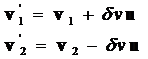 (23)
(23)
Now we can use equation 23 in equation 21 to solve for the value of dv.
![]() (24)
(24)
where the large dot stands for the dot product and equation 24 simplifies to:
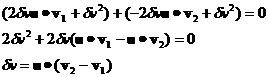 (25)
(25)
Equations 23 and 25 are a complete solution for the final velocities.
Since the animation is digital we will expect that most often the collision condition will be realized when the distance between the centers of the two spheres,r12, is less than D. To handle this we will increase the distance between the centers by the difference
![]()
by shifting each sphere in opposite directions by dr/2 along u. Thus we will move the centers by the vectors:
![]() (26)
(26)
Pressure
According to the references, the pressure reduction is proportional to the speed squared and the particle density, n (m-3):
![]() (27)
(27)
where m is the mass of the particle
or molecule and drift speeds, vd, were
already given in equations 4 and 5.
Therefore the pressure toward the horizontal center of the venturi will
be reduced. The lines of equal pressure,
isobars, are shown as vertical lines in the animation. The colors of these lines vary as the optical
spectrum from violet at the lowest pressure to deep red at entrance where the
pressure is lowest.