The Bohr Model of the Hydrogen Atom
Introduction
The model of the hydrogen atom created by Niels Bohr in 1913 was the simplest model that could explain all the spectroscopic data for hydrogen that was available at that time. It used just one quantum assumption that was beyond the classical physics that was well known at that time. Other than that, it also used the assumption that the electrons ran in circular orbits bound to a much heavier nucleus of the same (but oppositely signed) charge as the electrons.
Equations
The equation for the balance of electrostatic force between
the electron and the nucleus and the centripetal force needed to keep the
electron in its orbit is
![]() (1)
(1)
where m is the mass of the electron, v is its orbital speed, r is the radius of the orbit, e is the electric charge common to the electron and nucleus, and e0 is the permittivity of vacuum.
We can solve for v in equation 1 and obtain.
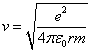 (2)
(2)
Using the result of equation 2, we can get the kinetic energy of the electron as:
![]() (3)
(3)
Taking into account that the potential energy of a motionless bound electron is:
![]()
then the total energy of the
electron is:
![]() (4)
(4)
So far we have not introduced anything about quantum mechanics but Bohr’s hypothesis was that the angular momentum, L=mvr, was quantized:
![]() (5)
(5)
where h is Planck’s constant and n is an integer greater than or equal to 1.
Now we can use equations 2 and 5 to compute the radius of
the nth electron orbit:
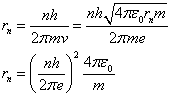 (6)
(6)
And then we use equation 6 to compute the energy of the
electron in the nth orbital state.
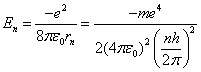 (7)
(7)
or expressed more simply in terms
of rn we have
![]()
![]()
![]()
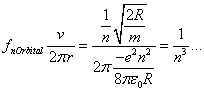
where R is known as the Rydberg.
For large n we can see that the difference of the energy levels is:
![]()
So that the emitted photon frequency is:
![]()
where
![]()
so that
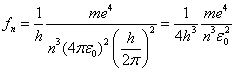
We can also use the above equations to compute the angular speed for the nth orbit. Repeating equation 5:
![]() (8)
(8)
Solving equation 8 for wn
we have:
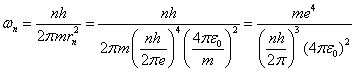
so that
![]()
Note that:
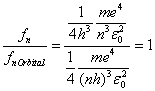 (9)
(9)
(9)
Equation 9 relates to the very important correspondence
principle which links classical and quantum mechanics in the limit of large n.
The emitted frequency for a single change of the quantum integer n equals the
orbital frequency of the electron as expected for classical physics.