Electromagnetic Energy Density in a Parallelepiped Cavity
Introduction
††††††††††† In order to fully understand the concept of black body radiation we should take a look at the energy associated with the modes of a black body cavity.† In doing this we will also develop an appreciation for the behavior of transverse waves in a parallelepiped cavity (PC) with reflecting inner walls.
Fields
††††††††††† Electromagnetic waves have polarization perpendicular to their propagation.† Their variation in space is sinusoidal. We want to choose waves that satisfy 2 requirements:
- The tangential components of the E fields must be zero at the boundaries.
- The vector electric field E must be perpendicular to the wave vector k.
- Since there is no free charge inside the PC, the divergence of E must be zero.
Trial functions for the Ex, Ey, and Ez components of the E vector could be chosen as
†††††††††††††††††††††††††††††††††††† 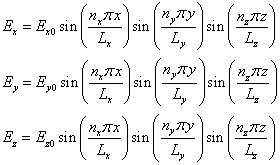 †††††††††††††††††††††††††††††††† (1)
†††††††††††††††††††††††††††††††† (1)
where nx, ny, and nz are positive integers and Lx, Ly, and Lz are the lengths of the (x,y,z) edges of the PC.† The three functions above satisfy the requirement 1.† However the divergence of the vector E is shown below:
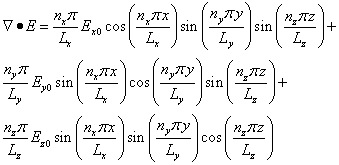 (2)
(2)
and this cannot be zero everywhere inside the PC.†
Note that the np/L quantities that multiply the terms in this expression are really the components of the wave vector, k:
†††††††††††††††††††††††††††††††††††††††††††††† ![]() †††††††††††††††††††††††††††††††††††††††††† (3)
†††††††††††††††††††††††††††††††††††††††††† (3)
and that we may choose Ex0, Ey0, and Ez0 to such that:
![]() ††††††††††††††††††††††††††††††††††††††††††† (4)
††††††††††††††††††††††††††††††††††††††††††† (4)
and thereby satisfy condition 2 above.
While itís not so obvious at first, if we choose the following functions for (Ex,Ey,Ez) we will also satisfy condition 3.
†††††††††††††††††††††††††††††††††††† 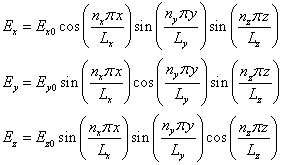 ††††††††††††††††††††††††††††††† (5)†††††††††††
††††††††††††††††††††††††††††††† (5)††††††††††† ![]()
because then the divergence of E becomes:
††††††††††† 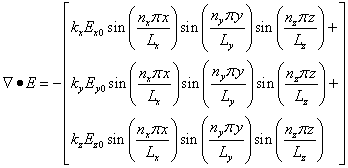 †††††††††††††††††††††††††††††††† (6)
†††††††††††††††††††††††††††††††† (6)
and by inserting expression 4 in equation 6 we see that equation 6 is indeed zero.
Finally we have to obtain the relative values of Ex0, Ey0, and Ez0.† We can use equation as well as one other equation to obtain Ex and Ey in terms for Ez.† The two equations are:
††††††††††††††††††††††††††††††††††††††††††††††††††† 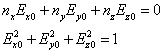 †††††††††††††††††††††††††††††††††††††††††††††† (7)
†††††††††††††††††††††††††††††††††††††††††††††† (7)
To simplify the results, we make the following substitutions
†††††††††††††††††††††††††††††††††††††††††††††††††† ![]()
so that equations 7 become:
†††††††††††††††††††††††††††††††††††††††††††††††††††††††† 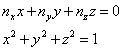 ††††††††††††††††††††††††††††††††††††††††††††††††††† (8)
††††††††††††††††††††††††††††††††††††††††††††††††††† (8)
Since there are 2 polarizations there are, of course, 2 solutions for x and y.
Let D represent the discriminant of the solutions of equations 8:
†††††††††††††††††††††††††††††††††††††††††† ![]() †††††††††††††††††††††††††††††††††††††† (9)
†††††††††††††††††††††††††††††††††††††† (9)
Then the fields are:
††††††††††††††††††††††††††††††††††††† 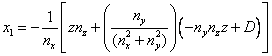 ††††††††††††††††††††††††††††††† (10)
††††††††††††††††††††††††††††††† (10)
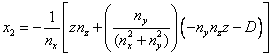 ††††††††††††††††††††††††††† (11)
††††††††††††††††††††††††††† (11)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††† 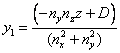 †††††††††††††††††††††††††††††††††††††††††††††††††† (12)
†††††††††††††††††††††††††††††††††††††††††††††††††† (12)
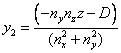 ††††††††††††††††††††††††††††††††††††††††††††††††††††† (13)
††††††††††††††††††††††††††††††††††††††††††††††††††††† (13)
In order to keep x and y real, we must choose any value for z that is less than
††††††††††††††††††††††††††††††††††††††††††††††††††† 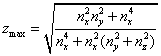 †††††††††††††††††††††††††††††††††††††††††††† (14)
†††††††††††††††††††††††††††††††††††††††††††† (14)
Reflections from the Walls
††††††††††† Does a reflection preserve the relationship between the k vector and the E field vector?† I believe it does because of the following comments.
- A reflection from. say the x=Lx wall just reverses the sign of the kx component of the k vector.
- The same reflection does not change the sign or value of the normal (Ex0) component of the E vector but it inverts the sign while leaving the value the same of both tangential components (Ey0 and Ez0).
Therefore, after reflection equation 5 becomes:
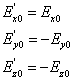
while
![]()
so that if E was normal to k before the reflection, it is still normal to k as shown below:
††††††††††††††††††††††††††††††††††††† ![]()
Plotting the Results
The fields themselves are vectors and therefore cannot be plotted in a clear quantitative way.† However, the electromagnetic energy density is a scalar and can be plotted.† For 2 dimensions, the ratio of Ex0 to Ey0 is
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ![]() †††††††††††††††††††††††††††††††††††††††††††††††††††† (15)
†††††††††††††††††††††††††††††††††††††††††††††††††††† (15)
so the fields can be described from equations 5 as:
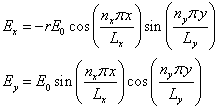 †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (16)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (16)
The scalar energy density is
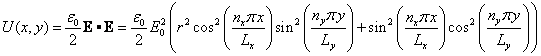 †(17)
†(17)
Equation 17 is plotted in the interactive animation.† An example of the results is shown in Figure
1.
† 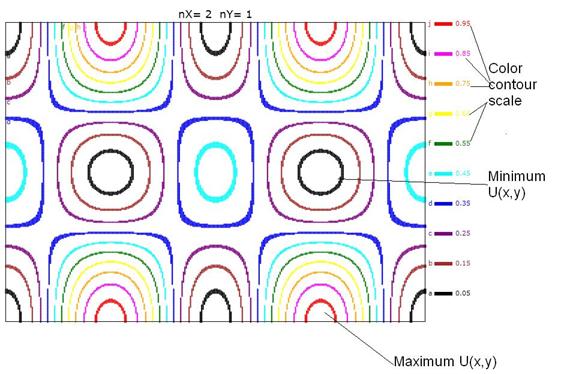
Figure 1: EM energy density for the mode nX=2, nY=1.† The colors of the
contours indicate the value of the EM energy density at any particular
location.†