Circle Rolling on an Ellipse

Introduction

The reason for this animation is that it teaches the use of vectors and differential calculus.

Math

To keep the circle on the ellipse as well as compute the number of turns of the circle as it rolls without slipping we need to compute the distance along the ellipse as well as the height of the center of the circle above the perimeter of the ellipse. The incremental distance along the ellipse is computed by the sum:

(1)

To compute dx and dy I use the parametric angular form:

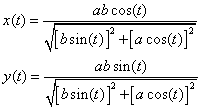(2)

where t is the angle from the horizontal axis of the ellipse, a is half-width of the ellipse, and b is the half-height of the ellipse.

I compute the values of x and y at both t, and t+dt where dt is a very small angle. Then

(3)

Let c be the radius of the circle. To compute the point (x_c ,y_c) to place the center of the circle we need to use the unit normal to the circle perimeter. First note that the unit tangential vector is:

(4)

where the x and y with hats on them are unit vectors. Another unit vector that is perpendicular to the tangential (and therefore normal to the ellipse perimeter) is:

(5)

Therefore, the point at which to place the center of the circle is:

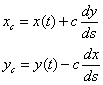(6)

Of course, the incremental angle (in radians) turned by the circle has to be:

(7)

The previous math will permit the calculation of the rotation and center position of the circle. However, the speed of the circle along the perimeter of the ellipse will vary. It is possible to choose a set of angles, angList, which pertain to uniform distances between steps of the circle. This is done by first numerically integrating ds above to find the length of the ellipse, eLen.

Then one may divide eLen by the number of angles desired, nAngs.

Then, as a first guess at the angle increment, use

Then divide dq by, say, 100 and for each angle desired iterate the following:

until

at which point one may add q to angList.