Circle Rolling on a rotating Ellipse

Introduction

The reason for this animation is that it teaches the use of vectors and differential calculus. It is very similar to “Circle Rolling on Ellipse” but it also teaches the use of superposition of motion.

Math

To keep the circle on the ellipse as well as compute the number of turns of the circle as it rolls without slipping we need to compute the distance along the ellipse as well as the height of the center of the circle above the perimeter of the ellipse. The incremental distance along the ellipse is computed by the sum:

(1)

To compute dx and dy I use the parametric angular form:

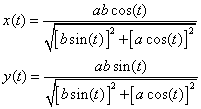(2)

where t is the angle from the horizontal axis of the ellipse, a is half-width of the ellipse, and b is the half-height of the ellipse.

I compute the values of x and y at both t, and t+dt where dt is a very small angle. Then

(3)

Let c be the radius of the circle. To compute the point (x_c ,y_c) to place the center of the circle we need to use the unit normal to the circle perimeter. First note that the unit tangential vector is:

(4)

where the x and y with hats on them are unit vectors. Another unit vector that is perpendicular to the tangential (and therefore normal to the ellipse perimeter) is:

(5)

Therefore, the point at which to place the center of the circle is:

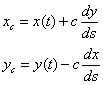(6)

Of course, the incremental angle (in radians) turned by the circle has to be the sum of the actual traction of the circle around the ellipse:

(7)

as well as the rotation of the normal to the ellipse as circle moves around the ellipse. The latter is computed by first taking the difference of two unit normal vectors:

(8)

where t is the angle of interest and dt is the step size to the next t.

The rotation angle associated with dn is:

(9)

The rotation of the circle for each step along the perimeter of the ellipse is then

(10)

The previous math will permit the calculation of the rotation and center position of the circle. However, the speed of the circle along the perimeter of the ellipse will vary. It is possible to choose a set of angles, angList, which pertain to uniform distances between steps of the circle. This is done by first numerically integrating ds above to find the length of the ellipse, eLen.

Then one may divide eLen by the number of angles desired, nAngs.

Then, as a first guess at the angle increment, use

Then divide dq by, say, 100 and for each angle desired iterate the following:

until

at which point one may add q to angList.

Superposing motion of circle onto a rotating ellipse

This can be done most simply by making the circle rolling on ellipse into a UserControl, EllipseAndCircle, into which the MainPage can pass the parameters, a and b, of the ellipse and radius, rad, of the circle as well as control the progress of the circle on the ellipse.

Thus, the Storyboard resides now on the MainPage and dictates the steps of the circle as well as the rotation of the ellipse. The MainPage also dictates the setup changes for EllipseAndCircle when the parameters a, b, rad change. When the ellipse rotates, the circle stays in contact with it since the motion of a UserControl is always superposed on the motion of the composite main object.