Derivation of equations for a circle on a plane in 3D

The equation for a point (x,y,z) in a plane described by vector (a,b,c) is

(1)

To describe a circle of radius r centered at (a,b,c) the following equation must also be true:

(2)

To simplify the notation of equations 1 and 2, I will define

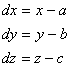
Then we have

(1’)

(2’)

We can eliminate dx from these equations and solve for dy in terms of dz:

If we redefine some terms this expression looks a lot simpler:\

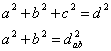where d is the distance from the origin to the plane

and then equation 3 becomes:

Obviously the range of dz to obtain real values for dy is:

Solving equation 1’ for dx we have except for the case where a=0:

(a<>0)

and solving equation 2’ when a=0:

(a=0).

There is also the case where both a and b are zero so that the range of dz is zero.

In that event, the circle is just parallel to the x,y plane at distance c from it: