Atom Motion in a Circular Two Dimensional Potential Well

Introduction

This is a hard sphere model of motion of atoms in a circular two dimensional potential well. It is the classical analog of tunneling of alpha particles out of an unstable nucleus.

Figures

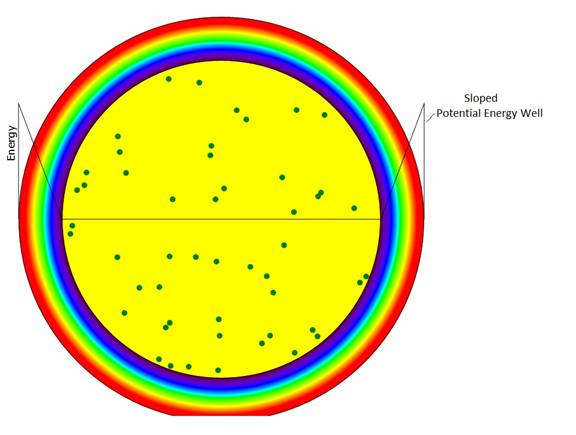
Figure 1: Sloped Potential Energy Well

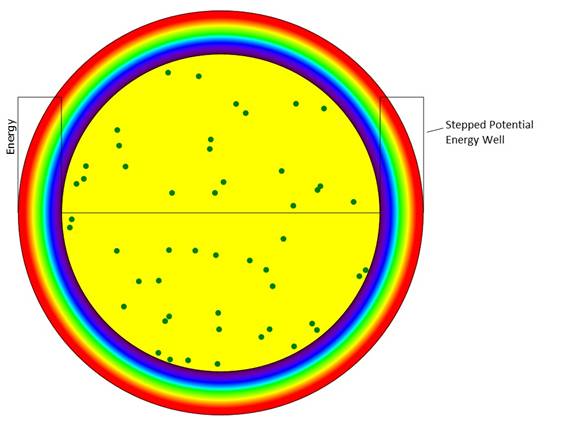
Figure 2: Stepped Potential Energy Well

Mathematics for Classical (particle) Case

Other than the atom-atom collisions that have already been well documented and the collisions with the outer radius which has also been documented, we have to take into account the effect of the sloped or stepped potential on the trajectories of the particles.

Sloped Potential

The motion in the sloped potential is easier to understand than that in the stepped potential so we'll do that calculation first. First we separate the particle velocity into its radial and tangential components:

where V is the velocity vector and r and t (with the hat) are the unit vectors in the radial and tangential directions at point (x,y)

and x and y (with the hats) are unit vectors in the x and y directions. Since the potential variation is radial the force, F, on the atoms is radial and therefore only the radial component of the momentum is affected.

where m is the mass of the particle and U is the potential energy. The expression for the sloped potential at radius r is

where r_I is the inner radius of the potential ring and r_O is the outer radius and r>r_I .

So an expression for F is

Therefore, for a single increment of time, the change in velocity is:

Stepped Potential

The effect of the potential step is to cause the velocity to instantaneously change direction similar to refraction of light at the surface of an index of refraction discontinuity. One may view this as a change of the radial component of the energy, E_r, of the particle. Recall the expression for the radial component of the velocity:

Prior to entering the potential, the radial energy is:

When entering the potential from r<r_I the new value of E_r becomes:

so that then the new value of v_r becomes:

When departing the potential from r>r_I the new value of E_r becomes:

so that then the new value of v_r becomes:

These equations are perfectly analogous to Snell's laws of refraction at the interface between two refractive media where the medium with the lower index of refraction is where the potential resides. Let our refractive indexes be:

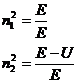
The angles with respect to the interface normal are given by the ratio of the tangential to the total velocity:

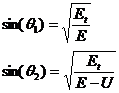
Therefore

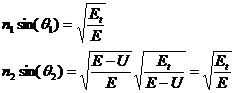
Equality of these last two equations constitutes Snell's law of refraction.

To derive Snell's refraction law for light waves we must make the ansatz that the tangential component of the wave vector must be the same on both sides of the interface in order to preserve the microscopic continuity of the fields. Since the wave vector is

and the values of |k| are

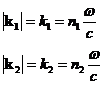
while the values of sin(q) are

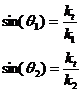
which, combined with the previous two equations results in

which is Snell's law of refraction.

Differential Equations for EM Waves and Quantum Waves

Electromagnetic wave equation with complex permittivity e

Try solution:

Rename ia to be k, the wave vector:

Then

Schrodinger equation with a potential, V, and kinetic energy E:

The fundamental difference is that the V-E term is usually real for the Schrodinger wave equation for one particle. If the potential is due to the force fields of many particles, then the potential could be complex because of the response times of these particles to the presence of the particle being analyzed.

Discussion of Solutions at a Discontinuity of the Parameters

In the two differential equations above, let's rename both factors emw² =n²k₀²and 2m(V-E)/h² =n²k₀² to make the two equations look the same:

We want to use only the differential equations to derive the solutions for E and y on both sides of the discontinuity. Let n=n₁ on the left side of the discontinuity and n=n₂ on the right side of the discontinuity and restrict the divergence to just one dimension, x. Further place the discontinuity at x=0. From the equations it's clear that the second derivative has a discontinuity at the interface

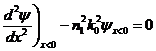
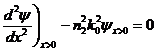
Subtracting these 2 equations we get:

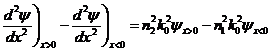
At x=0, the expression on the right hand side of the equation is a simple constant:

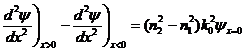
We may integrate this equation over a small range dx to obtain:

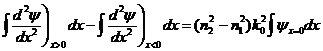
It's well known that the integral of a second derivative is just the first derivative:

Since the integral on the right side over a vanishingly small range of x is zero we then have the result that

With a totally similar argument we can show that

These are the two boundary conditions that are usually used for computing the values of y on both sides of the discontinuity.