Reflection of Waves from a Concave Spherical Mirror

Introduction

            Few people realize that reflection from a curved surface is a complicated physical process.  It involves both the radius of curvature of the wave front and the radius of curvature, rc, of the mirror.  These lead to variation of the phase lag or lead of the charges on the surface of the mirror which are responsible for the reflection. For a simple case where the axis of the mirror and the axis of the curved wavefront train coincide, the total axial phase lag that the mirror induces is twice the phase lag that would be experienced by a wave on a single passage to the mirror axis.  That will be explained by the Figures below as well as by the interactive animation which this document accompanies.

 

Figures:

  

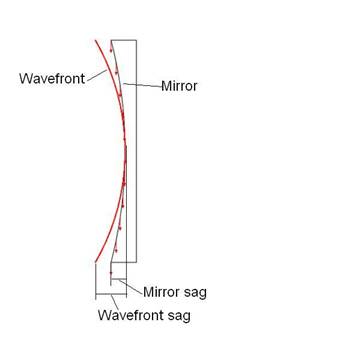
Figure 1: Mirror and wavefront departing from or arriving at the mirror.  The “sag” is the axial distance from the edge of either mirror or wavefront to the axial point at the center of either.  In order to either collimate (provide light with planar wave fronts) arriving from a point source or focus already collimated light, the sag of the wave front must be twice that of the mirror as shown.  For either case, the focal distance will be twice the radius of curvature of the mirror.

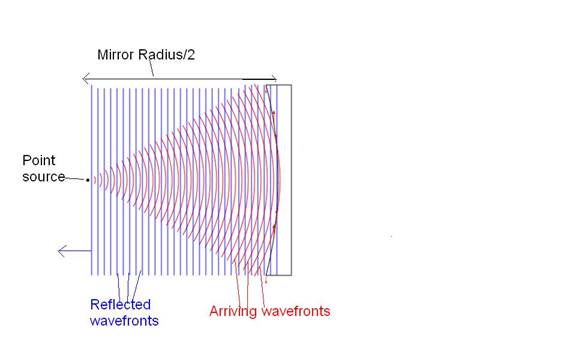
Figure 2: Showing both the Arriving wavefront train and the Reflected wavefront train.  In this case the wavefronts originate from a point source located at distance rc/2 away from the axial point of the mirror.  As a result of their Arriving wavefront source distance being rc/2, the Reflected wavefronts are perfectly planar.

 

Figure 3: Same as Figure 2 except now the arriving wavefront train(blue)  is planar while the departing wavefront train (red) has shapes that correspond to sections of the surface of a sphere which has diminishing radius as the wavelets converge toward the point focus shown.  As a result of the Arriving wavefronts being planar, the Reflected wavefronts converge to a point that is distance rc/2 from the axial point on the mirror.

 

 

Computations:

 

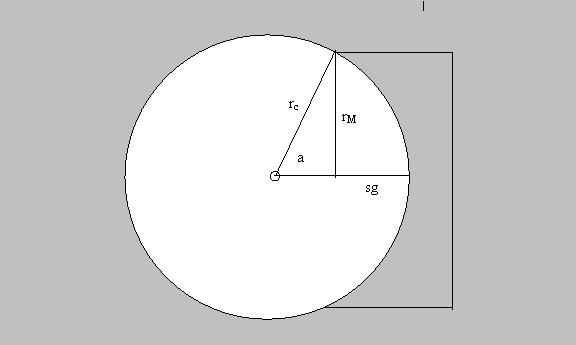
Figure 4: Geometry for computing the sag of a spherical concave mirror. See below for details.

From Figure 4, it’s obvious that

                                                                                                                      (1)

and that the horizontal line from the mirror’s center of curvature to the axial point  of the mirror has length rc.  Therefore the sag, using the Pythagorean theorem, is:

                                                                                                               (2)

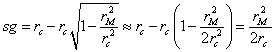However, if rM is significantly less than rc then we can make a Taylor series expansion of equation 2 and obtain the following sag approximation:

                                                   (3)

A simple exact expression for sag is also obtained from the geometry of Figure 4:

                                                                                                               (4)

Equation 3 is sufficiently accurate for both the mirrors and the spherical wavelets in our present animation.