The Best Trajectory to Negotiate a Turn in the Road

Introduction

This animation will show the resulting lateral accelerations for two types of curve. First is the ideal curve that is the largest one that can stay within the bounds of the lane. Second is a curve that is adjustable by the user. For both types of curve, the speed profile is adjustable via a smooth Bezier curve. We will also discuss a trajectory that is safer than the ideal curve.

Figures

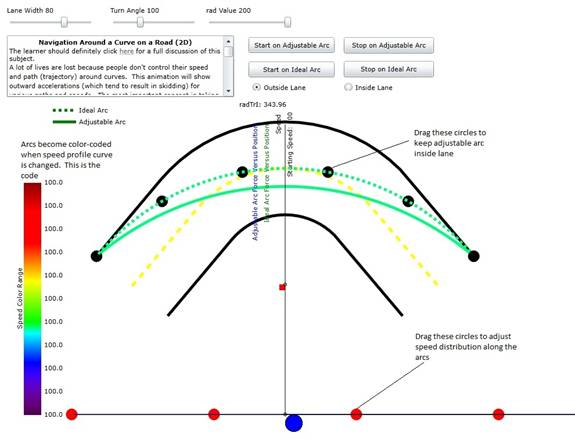
Figure 1: Diagram of the animation describing how to use the adjustable arc and speed profile.

Computing the ideal arc

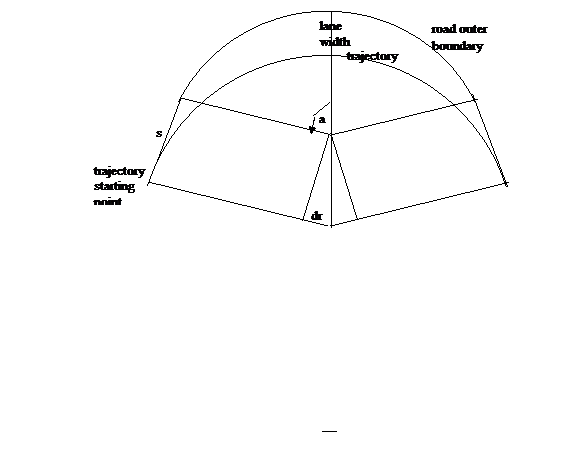
Figure 2: Diagram of the turn outer boundary and the possible trajectory. Symbol a is half of the total turn angle while symbol s is the straight line distance from the start of the curved trajectory to the start of the arc that represents the outer boundary of the road. as can be seen, the parameter dr is the difference between the trajectory radius and the road outer bound radius.

It is obvious from the figure that the value of dr is:

$d r = \frac{s}{\tan a}$

(1.5)

Also the lane width, w, is

$w = \frac{s}{\sin a} - \frac{s}{\tan a}$

(1.6)

From equation (1.6) we may compute s in terms of w and a:

$s = w \frac{\sin a}{1 - \cos a}$

(1.7)

and from equations 1.5 and 1.7 we can compute dr:

$d r = w \frac{\sin a}{\tan a (1 - \cos a)} = w \frac{\cos a}{1 - \cos a}$

(1.8)

Computing the Lateral Acceleration

I assume we have a parametric path in 2D space:

$x_{i}, y_{i}$

(1.1)

where i is the counter integer for successive points, what is the transverse acceleration needed to stay on the path?

The transverse acceleration depends on the rate of change of the vector normal to the path. If we just have a listing of $x_{i}, y_{i}$ then we can make an estimate of the change of the unit normal, n, by taking the following quantities:

First the local normal is computed from:

$\begin{array}{l} d x = x - x_{0}, d y = y - y_{0} \\ d s = \sqrt{d x^{2} + d y^{2}} \\ n = - \frac{d y}{d s} x + \frac{d x}{d s} y \end{array}$

(1.2)

where x₀ and y₀ are immediately previous values of x,y and x and y are the present values. In order to compute the change in normal vector we need to have saved an immediately previous value of n as n₀

Then

$d n = n - n_{0}$

(1.3)

is the local change. The acceleration a normal to the path then is

$a = {(\frac{d s}{d t})}^{2} \frac{d n}{d s}$

(1.4)

where ds is the spacing along the path of the points and dt is the time increment between points. Please take note that it is not assumed that the curve is part of a circle.

A Safer Trajectory: 2/3-1/3 rule

It is usually safe enough to start the turn at the outer bound of the lane. But t is not safe to exit at the outer bound. For that reason the two third-one third rule is suggested. To follow this rule, the operator hits the apex when he/she has completed 2/3 of the angle of the curve. That means that he/she can exit the turn in the middle of the lane rather than the outside of the lane as shown in Figure 3. This leaves a safety margin in case the exit is blocked by other traffic or debris.

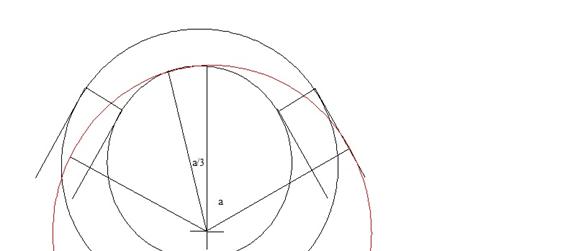
Figure 3: The entry to the curve is at the right and the exit is at the left.

The red curve is the trajectory that agrees with the 2/3-1/3 rule.