The required focal accuracy for a given digital camera sensor resolution
Introduction
I have examined the subject of depth of field[1] in Wikipedia and I found it much more difficult to understand than necessary and not specialized to the subject of digital CCD imaging. Therefore I decided to develop my own formula. I will use the same symbols for the quantities as in the Wikipedia article but try for a better geometric understanding of being out of focus.
Geometry
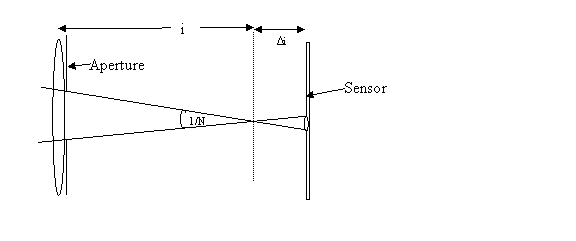
Geometry used for this
discussion. The outer rays of light
through the aperture form the surface of a cone that has vertex angle 1/N (expressed
in radians) where N is the f number of the aperture/lens combination. The image distance from the lens is denoted
as symbol i. The sensor plane is located distance DI from the image plane.
The important thing to note from the above drawing is that the outer rays of light through the aperture form the surface of a cone that has approximate vertex angle 1/N where N is the f number of the lens-aperture combination i.e. N=f/A where f is the lens focal length and A is the aperture diameter. Also, for N larger than 2, the diameter of the base of the cone at the sensor is approximately d=Di/N (error in this approximation is less than 1%).
Using the thin lens equation
We now need to relate the image distance error, Di, to the subject distance error, Ds.
The thin lens equation is
![]()
We need the derivative of i with respect to s:
![]()
Now we need to apply this derivative to find the diameter of the base of the cone at the sensor in terms of subject distance variation:
![]()
For almost all cases a good approximation for the image distance, I, is i=f.
![]()
I would generally like to know d in terms of the fractional variation in the subject distance so I rewrite the equation as.
![]() (1)
(1)
Results and conclusions
The above expression is a coefficient, f2/(sN), times a fractional variation of s. Taking some typical numbers for subjects far away use f=55 mm, N=5.6, and s=5.5 meters (5500 mm), we get
![]() (far subjects)
(far subjects)
And for closer subjects take s=0.55 meters and get:
![]() (near subjects)
(near subjects)
Thus, for this chosen f and N, for far subjects, items at Ds/s=10% from the in-focus subject plane will have cone base diameters of 0.01 mm. For near subjects, items at Ds/s=10% from the in-focus subject plane will have cone base diameters of 0.1 mm.
Now let me compute what this means for blurring at the sensor plane. Let me assume that we have 2400 pixels distributed over a 24 mm width so that the pixel spacing is 0.01 mm.
Since the cone base diameter for far subjects is also 0.01 mm, that means that, about half the time, the far subject light from points 10% from the main subject plane falls on 2 pixels. Therefore the limit to get ideal digital resolution for this setup is a subject distance variation of Ds/s =10%.
Since the cone base diameter for near subjects with a 10% distance variation is 0.1 mm, that this near subject light falls on 10 pixels. Therefore the limit to get ideal digital resolution for this setup is a subject distance variation of Ds/s =1%. One immediately sees the need to use large f numbers, N, for near subjects.
Critique
Since the
image distance, i, gets considerably larger than f
for really close subjects (typically about 1.4 f is the limit), the actual cone
base diameter is larger than that given by equation 1. Therefore, the fractional subject distance
range for ideal digital focusing is even less than that computed above by up to
a factor of 1/(1.4)2 = 1/2.