Levitation of a Cylindrical Magnet Using Diamagnetic Material

Introduction

Almost everyone who has handled 2 magnets knows that one magnet will lift the other against Earth's gravity if the closest end poles are of the opposite type (i.e. one is North and the other is South) and the pole spacing distance is small enough. But those same people know that the spacing where magnet 1 just barely supports magnet 2 is extremely unstable. If the lower magnet is brought to that point and then let go, it either falls to the floor or it violently collides with the attracting pole of the upper magnet. Diamagnetism gives us a way around this dilemma. Diamagnetism creates a weak opposing force which depends on the speed toward the diamagnetic slab (DS). Thus, any lifted magnet motion toward the slab is usually slowed to zero speed before it collides with the slab. If the lifted magnet (LM) is placed between two horizontally oriented slabs, both the motion toward the upper magnet and the motion toward the floor are retarded. The spacing between the slabs is determined by their diamagnetism whish is really dependent in their electrical conductivity in the horizontal plane. The diamagnetism handles the stability in the vertical direction. Once that is done, the lifted magnet is also stable in the radial direction since there is always a small inward radial force between magnets that are almost aligned on their axes.

Calculation of Dynamic Forces on Levitated Magnet of Diamagnetic Slabs.

What we have is the levitated magnet with its axis aligned the vertical direction and it moves either up or down along the vertical direction. When it moves toward a DS, all of the electrons in the DS feel an additional force

$F = q v \times B$

(1.1)

where q is the electron charge, v is the velocity of the magnet with respect to the DS and B is the local field in the DS. Since v has only a z component, and B has no circumferential component, the cross product becomes

$F = q v_{z} B_{r}$ $ϕ$ (1.2)

where B_r is the radial component of the magnetic field due to the LM and where $ϕ$ represents the circumferential direction. We can interpret v_zB_r as the magnitude of an electric field in the $ϕ$ direction. Then we can write the current density due to the motion of the LM toward the DS as

$J = σ v_{z} B_{r}$ $ϕ$ (1.3)

where σ is the electrical conductivity of the DS.

We can integrate over this current density to obtain a magnetic field that opposes that of the LM. But, more simply, we can use the following equation to directly obtain the force that the DS applies to the LM. The basic expression for a small force element on a current carrying wire due to an external magnetic field, B, is:

$δ F = i δ l \times B$

(1.4)

where i is the current in the wire and δl is length of the segment of wire under discussion For our case points δl points along the J (or $ϕ$ direction). The cross product in equation (1.4) has two possible components, a radial component due to B_z and an axial (z) component due to B_r. The radial component can only slightly change the orbit radius of the electrons which are already strongly rotating due to the static B_z. It is the axial component due to B_r that will result in the repulsion of the plate or magnet as they approach each other. To get the total repulsion force, we have to convert the current i to an integral over J and integrate over δl. The latter integral is easy since all the electrons are orbiting around the magnet axis

$\oint δ l (r) d ϕ = 2 π r$

(1.5)

To convert i to a current density we must take a small differential area around the point (r,z)

$i = J d r d z$

(1.6)

Then the expression for the total repulsive force becomes:

$F_{z} = (2 π) \iint r J B_{r} d r d z = (2 π) \iint r σ v_{z} B_{r}^{2} (r, z) d r d z$

(1.7)

where the integration is over the full thickness and radius of the slab.

If instead, we want the force element at coordinates (r,z) for a single ring of the DS in order to make a contour plot of these elements, that force element is:

$δ F_{z} (r, z) = 2 π r σ v_{z} B_{r}^{2} (r, z)$

(1.8)

Equations of Motion

The dynamic and static forces discussed in the previous section would be enough to describe the position and speed of a small magnet that has no mass. However, since real magnets have mass and therefore momentum, the latter has to be taken into account for computing the position of the magnet versus time. The equation of motion is

$m \frac{d v_{z}}{d t} - b v_{z} - m g + k (z - z_{0}) = 0$

(1.9)

where m is the magnet mass, b is the coefficient of the dynamic forces due to the eddy currents, g is the (downward) acceleration of gravity, k is the coefficient of the slope of the static forces on the magnet and z₀ is the "neutral" height where the small magnet would have no motion. From the definitions above, we can write:

$k z_{0} = - m g$

(1.10)

and equation (1.9) becomes:

$\frac{d v_{z}}{d t} - b v_{z} + k z = 0$

(1.11)

For a more complete description let's assume that a sinusoidally varying force due to a small coil drives the levitated magnet up and down around its neutral position just as in the animation. (Otherwise we could assume that the LM suffers a small upward or downward force impulse.) Then equation (1.11) becomes:

$m \frac{d v_{z}}{d t} - b v_{z} + k z = F \cos ω t$

(1.12)

We solve equation (1.12) by the assumption

$z = Real (z_{a} e^{i ω t})$

(1.13)

where z_a is the (presently unknown) complex amplitude of the motion and ω is its radian frequency and t is time.

Substituting equation (1.13) into (1.12) we have the following:

$- m ω^{2} z_{a} - i b ω z_{a} + k z_{a} = F$

(1.14)

The solution for z_a is:

$z_{a} = \frac{F}{k - i b ω - m ω^{2}}$

(1.15)

Then using equation (1.15) in (1.13) we have:

$\begin{array}{l} z = Real (z_{a} e^{i ω t}) = Real (\frac{F e^{i ω t}}{k - i b ω - m ω^{2}}) \\ = F Real (\frac{\cos ω t + i \sin ω t}{k - i b ω - m ω^{2}}) = F Real (\frac{(\cos ω t + i \sin ω t) (k + i b ω - m ω^{2})}{{(k - m ω^{2})}^{2} + {(b ω)}^{2}}) \\ = F \frac{(k - m ω^{2}) \cos ω t - b ω \sin ω t}{{(k - m ω^{2})}^{2} + {(b ω)}^{2}} \end{array}$

(1.16)

Caveat:

Equation (1.16) is a simplified version of the actual motion. The problem is that, even for small displacements from equlibrium, z₀, k is a significant function of z and so is b. That changes this problem from being a simple harmonic oscillator into an anharmonic oscillator. And that is beyond the scope of the present document.

Figures

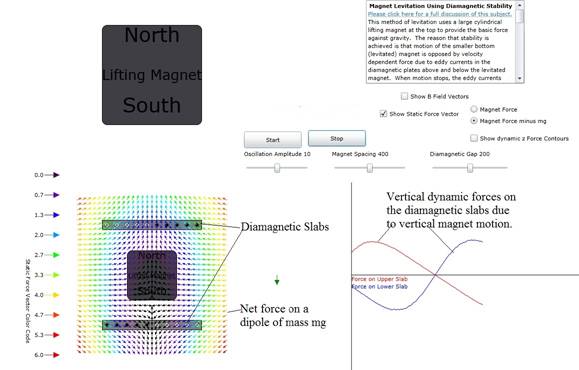
Figure 1: showing the entire animation with all options.

Figure 2: Static magnet force vectors on small dipoles located at the root of the arrows.

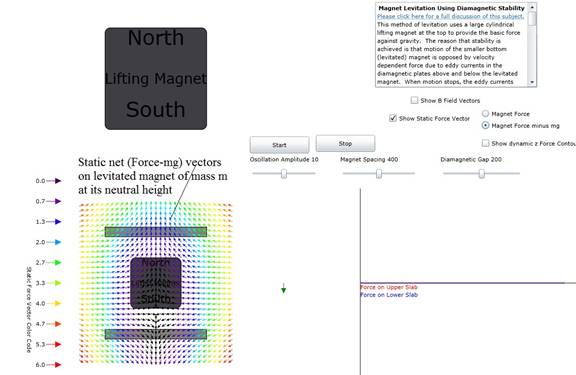
Figure 3 Static magnetic force vectors after subtracting off the force on gravity on a small magnet. Note that the arrows are violet at the center of the magnet since this shows its neutral levitated position.

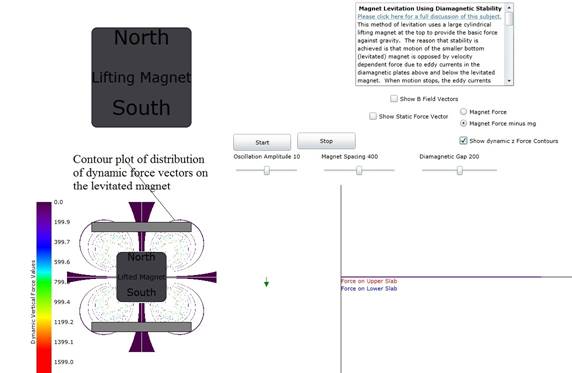
Figure 4: Dynamic z force contour plot, assuming a constant magnet z velocity, at points where a diamagnetic material may be located.

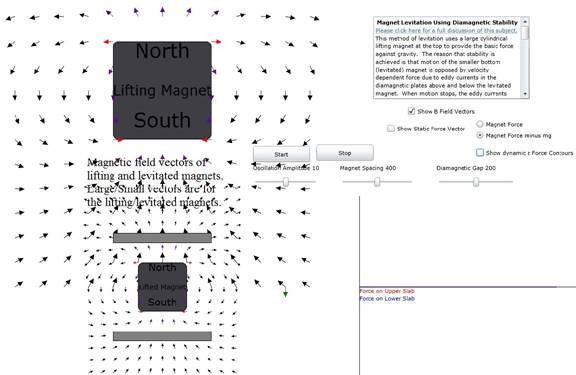
Figure 5: Static magnetic field vector plot for both lifting and levitated magnet. The color code is the same as that for Figure 3.