Radiation Energy Received by a Relativistic Absorber
Introduction
One runs into a logical dilemma when the following scenario is considered. The light source emits electromagnetic radiation at frequency f0 in the form of a highly collimated beam. The collimation is good enough that a distant fast-moving absorbing body moving away from the source is able to collect all of the emitted radiation. However, because of the Doppler effect, the frequency of the absorbed radiation is reduced by the factor
![]() (1)
(1)
where the relative speed of the absorbing body is v, c is the speed of light, and b is the standard contraction for the ratio v/c. Obviously, since photon energy is hf, where h is Planck’s Constant, and photon numbers are conserved, the light energy per unit time that can be absorbed by detectors and used as heat on the body is reduced by the factor (1-b). The dilemma is the question, where did the energy fraction b go?
Resolution of the Dilemma
For simplicity it is best to first consider the energy received per unit distance of the body’s travel away from the source. Then, if the radiation intensity is I0 watts per square meter, the total amount of radiation energy that can be received as heat by the detectors per unit area and distance is:
![]() (Joules
meter-3) (2)
(Joules
meter-3) (2)
where I0 is the power per unit area emitted by the source and
the incremental body distance traveled is dx.
There is another way that the incoming light energy is used: That is the radiation pressure that the photons exert on the body. This radiation pressure exerts an energy per unit area and distance traveled:
![]() (Joules meter-3) (3)
(Joules meter-3) (3)
EKE is the classical kinetic energy of the body and where m is the body’s average mass per unit area and v is the speed of the body. So the radiation pressure’s effect is to increase the body’s speed and therefore the kinetic energy of the body.
Taking the sum of equations 2 and 3, we have the total energy per unit area and distance:
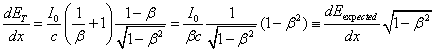 (4)
(4)
Where dEexpected/dx is energy received per unit area and distance even when there are no Doppler shift effects. Therefore, despite the Doppler frequency shift which is linear in speed v, in the classical limit where b<<1, we have, to order b2, the expected result for the total energy received per unit area and distance.