Driven LCR Oscillator Animation
Introduction
The Driven LCR oscillator (LCR) is an exact analog of the Forced Harmonic Oscillator shown under the Mechanics chapter. Its behavior goes a long way toward understanding the electrodynamics of the real world.
Calculations:
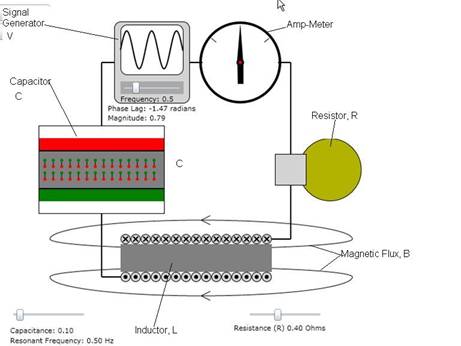
Figure 1: Circuit diagram showing the Signal Generator,
Vs, Capacitor C, Resistance, R, and Inductor, L. R is
a light bulb which changes brightness as current flows through it.
The picture above shows the
important parameters of the LCR. They include a Capacitor, C with variable capacitance,
a damping Resistor (shown here as
Spring Constant=k
a light bulb with a variable resistance R ohms) and an
Inductance, L, which has an inductance of 1 Henry, at the bottom. The function of the capacitor is to trade
off energy between itself and the magnetic field of the inductance and the
function of the light bulb is to realistically absorb energy from the circuit. Again, the layout of this electrical
circuit is exactly analogous to the layout of the Forced Harmonic Oscillator
under the Mechanical chapter.
The equation that describes the charge of the capacitor is:
![]() (1)
(1)
where Vs is the voltage
provided by the signal generator.
To solve equation 1 we make the substitution:
![]() (2)
(2)
where the real part of q will be the charge on the capacitor, i is the square root of -1, Real[] denotes the real part of the resulting value, Q is the peak capacitor charge, t is time. Using equation 2 in equation 1 we have very easily:
![]() (3)
(3)
For notation convenience we make the definitions:
![]() (4)
(4)
![]() (5)
(5)
Using equations 4 and 5 in equation 3 we have
![]()
or
![]() (6)
(6)
from which using equation 2 we have
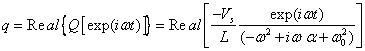 (7)
(7)
Separating Q into real and imaginary parts we get:
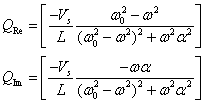 (8)
(8)
Note that, if Vs<0, the imaginary part of Q is
always negative and the real part is negative when w>w0 and
positive when w<w0.
Computing the real part of equation 7 we obtain:
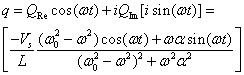 (9)
(9)
We can obtain the phase of q using the following equation:
![]() (10)
(10)
where the function atan2 evaluates
the arc tangent on the interval (0 -> -p)
without the usual discontinuity of the arctangent.
Dielectric Slab Animation
![]()
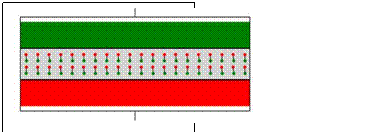
Shown above is the dielectric slab in the capacitor gap. The color and depth of the charge in the two
plates indicate both the sign and the value of their charge. The rotation angle of dipoles, which are
shown as dumbbells with a red end and a green end, is animated. When the
imposed electric field is large, they are aligned anti-parallel to the electric
field. This is the effect of a
dielectric slab in a capacitor: Since the slab’s dipoles align opposite
to the imposed electric field they cancel a large fraction of that field and
therefore a larger charge on the red and green plates is required to achieve
the same voltage across the capacitor.
When the imposed electric field is small or zero, the orientation of the
dipoles becomes random as can be seen from the animation
Summary
The meaning of equation 10 is that the capacitor charge, q,
will follow the voltage applied by the signal generator and will thus have a
cosine periodic behavior with the phase lag given in equation 10.