Distortions and Waves in Elastic Media

Introduction

This animation will explore waves in elastic media at the individual atom level. The elastic here will be represented by the massive nuclei generally held at some equilibrium distances by springs which really represent the electron clouds surrounding the nuclei. When an elastic wave is introduced, the distances between the nuclei change periodically with both time and space. For simplicity, we will assume what is called plane waves where entire lattice planes move with respect to their neighboring planes. The most important goal here is to help visualize the kinetics of the waves. We will work with two types of wave:

1. Transverse waves: Here the lattice planes slide parallel to their surface with respect to both their nominal position and time so that the distance between planes remains constant.

2. Longitudinal waves: Here the lattice planes move along their normals so that the distance between planes varies sinusoidally with respect to both nominal position and time.

Figures:

Figure 1: Transverse Elastic wave. In this case the mode number is 3 so there are 3 nodes in the lattice positions.

Figure 2: Longitudinal Elastic wave. In this case the mode number is 3 so there are 3 nodes in the lattice plane horizontal positions.

from their equilibrium length of Δl and a difference stretch of 2δl.

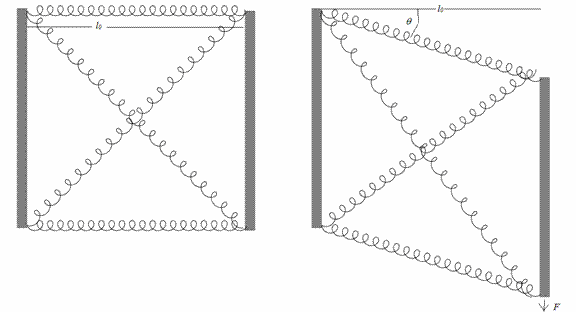
Figure 3. Shear Load Cell. The cell on the left is not loaded and its horizontal lengths are l₀ while the diagonal spring lengths are l₀(2)^1/2. The cell on the right has enough downward force applied to its right side loading plate to cause the horizontal springs to deflect to angles θ. In order to obtain reasonable ratios of shear to normal modulus in a 3D model, we would need to include the 4 body diagonal springs of the cubic cell but these are not shown here.

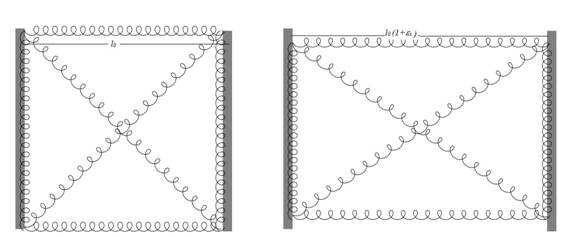
Figure 4: Normal Load Cell. Normal extensional strain of a cell similar to the one in Figure 3. The cell on the left is unloaded while the cell on the right has a strain of ε_x=0.3. The Poisson ratio of the strained cell is 0.4 causing a shortening of the vertical springs. In addition to the front face shown here, the restoring force for the normal strain includes either the top or bottom face of the cube with its diagonal springs. In order to obtain reasonable ratios of shear to normal modulus in a 3D model, we would need to include the 4 body diagonal springs of the cubic cell but these are not shown here.

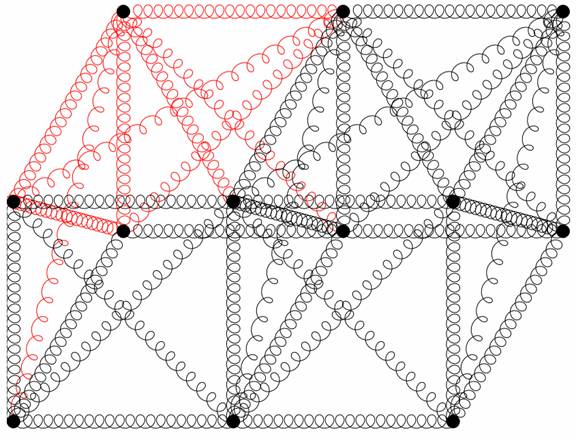
Figure 5: Showing a solid made up of nuclei and springs. It is assembled from 3D unit cells. Each unit cell contains a springs along the (x,y,z) axes as well as 2 diagonal springs on each of the three faces adjacent to the (x,y,z) axes of the cell. In this case, the 9 springs of the first unit cell are colored red. The dangling springs of the edge cells which would be there when the entire solid is made up of 3D unit cells are made invisible for clarity. Four body diagonal springs that should be included are omitted for clarity. Four body diagonal springs that should be included are omitted for clarity. It is very important to understand how many of each type of spring are contained in a solid made up of (nx,ny,nz) cells.

Math

A. Shear Modulus of Spring Model

A spring model of a solid that results in a reasonable shear modulus is shown in Figure 3. On the sheared version on the right, the lengths of the previously horizontal springs are increased to

$l = \frac{l_{0}}{\cos θ}$

(1.1)

Since the expansion of the cosine for small θ has no linear terms, the previously horizontal springs have no effect on the small deflection shear modulus.

Using the law of cosines of the angles opposite the diagonals to get the lengths of the diagonal springs we have:

$\begin{array}{l} l_{d 1} = \sqrt{l_{0}^{2} + l^{2} - 2 l_{0} l \cos (π / 2 + θ)} \\ l_{d 2} = \sqrt{l_{0}^{2} + l^{2} - 2 l_{0} l \cos (π / 2 - θ)} \end{array}$

(1.2)

where d1 denotes the longer diagonal and d2 denotes the shorter diagonal.

Note that

$\begin{array}{l} \cos (π / 2 + θ) = - \sin θ \\ \cos (π / 2 - θ) = \sin θ \end{array}$

(1.3)

Both diagonal springs exert a linear restoring force when the shear load, F, is applied to the right side plate. Since θ<<1, sin θ = θ, and we may expand equations (1.2) to first order and obtain:

$\begin{array}{l} l_{d 1} \approx \sqrt{l_{0}^{2} + l^{2}} (1 + \frac{l_{0} l}{l_{0}^{2} + l^{2}} θ) \\ l_{d 2} = \sqrt{l_{0}^{2} + l^{2}} (1 - \frac{l_{0} l}{l_{0}^{2} + l^{2}} θ) \end{array}$

(1.4)

Further, since cos θ is to a second order approximation 1, l=l₀, so that equations 1.12 become:

$\begin{array}{l} l_{d 1} \approx \sqrt{2} l_{0} (1 + \frac{l_{0}^{2}}{2 l_{0}^{2}} θ) = l_{d} (1 + θ / 2) \\ l_{d 2} = \sqrt{2} l_{0} (1 - \frac{l_{0}^{2}}{2 l_{0}^{2}} θ) = l_{d} (1 - θ / 2) \end{array}$

(1.5)

where l_d=l₀(2)^1/2 is the unloaded diagonal length.

If κ_dis the spring constant for the face diagonal springs then the tensile restoring force then for d1 is

$F_{d 1} = κ_{d} (l_{d 1} - l_{d}) = κ_{d} θ l_{0} \sqrt{2} / 2$

(1.6)

while the compressive restoring force for d2 is

$F_{d 2} = κ_{d} (l_{d 2} - l_{d}) = - κ_{d} θ l_{0} \sqrt{2} / 2$

(1.7)

For small θ, both of these restoring forces act at 45 degrees from the vertical against the downward force applied to the load cell. The total upward force is then:

$(F_{d 1} - F_{d 2}) s i n (π / 4) = \frac{κ_{d} θ l_{0} \sqrt{2}}{\sqrt{2}} = κ_{d} θ l_{0}$

(1.8)

This will result in a shear modulus, G, of

$G = \frac{F}{A θ} = \frac{κ_{d}}{l_{0}}$

(1.9)

where A is the area of the right hand plate of the load cell.

B. Normal (or Young's) Modulus of Spring Model

Here it's important to first decide what constitutes a unit cubic cell. A unit cubic cell consists of enough cube faces such that we could build an entire lattice from a group of these. Such a unit cell is shown, colored red, in Figure 5. As such, it will be sufficient to include the top horizontal spring of the back face, the bottom spring of the left face, and the vertical spring of the back face. This is sufficient to let us stack the unit cells vertically or horizontally and extend the lattice.

For the normal forces we need to the diagonal springs of the top face, the left face, and the back face. For the force in the x direction we need only to include the diagonal springs of the top and back faces.

The normal (tensile and compressive) force in the x direction for a load cell turn out to be:

$F_{N} = δ l (κ + 2 κ_{d})$

(1.10)

where the 1 relates to the top horizontal spring and the 2 relates to the 4 diagonal springs of the top and back faces. This results in a Young's modulus of

$E = \frac{F_{N}}{A} \frac{l_{0}}{δ l} = \frac{(κ + 2 κ_{d})}{l_{0}}$

(1.11)

Equations (1.9) and (1.11) would result in a ratio of G to E of

$\frac{G}{E} = \frac{κ_{d}}{κ + 2 κ_{d}}$

(1.12)

and, for this case, where volume is held constant, the ratio should be 1/3 but we expect that κ_d<κ so our result is less than 1/3. But we haven't included the body diagonal springs of the cell and these should be used in a 3 dimensional solid.

C. Shear Modulus Including Cell Body Diagonals.

If we let the top-upper-left vertex of the cell remain at the origin (0,0,0) and make the nominal side length l₀, then the other vertices are at ( 0,0,l), (0,l,l), (0,l,0) which completes the left face vertices and at (l,0,0), (l,0,l), (l,l,l), and (l,l,0) which completes the right face vertices. The body diagonals always have one coordinate on the left face and one on the right face. They are (stating the right face second):

(0,0,0)-(l,l,l), (0,0,l)-(l,l,0), (0,l,l)-(l,0,0), and (0,l,0)-(l,0,l).

When the cube is under a shear load, the y values of the body diagonal ends on the right face are deflected downward by θ since all the side lengths are l. Therefore the set of diagonals become

(0,0,0)-(l,l+ θ,l), (0,0,l)-(l,l+ θ,0), (0,l,l)-(l, θ,0), and (0,l,0)-(l, θ,l).

The lengths of the diagonals become:

$l_{d} = l \sqrt{2 + {(1 + θ)}^{2}} \approx \sqrt{3} l (1 + θ / 3)$

(1.13)

The y components of the diagonals are +/-l and their nominal lengths are the square root of 3 so the force along the y direction will be:

$F_{d y} = κ_{b d} l \frac{\sqrt{3}}{3} θ (\frac{l}{\sqrt{3}}) = \frac{κ_{b d} θ l_{0}}{3}$

(1.14)

where κ_bd is the spring constant of he body diagonal springs.

Since there are 4 of the springs and all are working to restore the shear to zero, the total force is

$F_{d} = \frac{4}{3} κ_{b d} θ l_{0}$

(1.15)

This is to be added to the force produced in the previous section by the face diagonals

$F_{d y} = θ l (κ_{d} + 4 / 3 κ_{b d})$

(1.16)

and will result in a shear modulus of

$G = \frac{F_{d y}}{A θ} = \frac{1}{l_{0}} (κ_{d} + 4 κ_{b d} / 3)$

(1.17)

D. Normal Modulus Including Cell Body Diagonals.

The only difference from the shear case is that the strain adds increment εl₀ to the x coordinate instead of the y coordinates of the ends of the diagonals on the right face of the cube. So we again have an additional restoring force of

$F_{d} = \frac{4}{3} κ_{b d} ε$

(1.18)

and the total Young's modulus becomes:

$E = (κ + 2 κ_{d} + 4 κ_{b d} / 3) \frac{1}{l_{0}}$

(1.19)

Then the ratio of G to E becomes:

$\frac{G}{E} = \frac{(κ_{d} + 4 κ_{b d} / 3)}{(κ + 2 κ_{d} + 4 κ_{b d} / 3)}$

(1.20)

Poisson Ratio

Since the equation for the relation between E and G is

$\frac{E}{G} = 2 (1 + ν)$

(1.21)

where ν is Poisson's ratio we obtain the following result for ν:

$ν = \frac{E}{2 G} - 1 = \frac{(κ + 2 κ_{d} + 4 κ_{b d} / 3)}{2 κ_{d} + 8 κ_{b d} / 3} - 1$

(1.22)

We expect ν to be between 0 and 1/2 for an isotropic material. If all three spring constants are equal, then Poisson ratio =0. If we include the fact that κ will be smaller for the diagonal and body diagonal springs, we would have gotten a larger Poisson ratio.

Waves

The main goal of this section is to compute the wave speeds and oscillation frequencies of the transverse and longitudinal mode of oscillation. We will make use of the small angle approximation, sin θ=θ where θ is expressed in radians.

In the long wavelength limit where λ>>l₀, the wave spatial and temporal variation can be expressed as

$u = A \sin k_{x} x$

(1.23)

where u=y for the transverse wave and u=x for the longitudinal wave, A is the amplitude of the wave, and k_x is the wave number of the particular oscillation.

1. Longitudinal Wave Speed and Frequency

In this case the particle displacement is along the direction of the wave. First you need to realize that a constant value of du/dx across the entire solid is just a simple displacement of the solid and results in no spring compression or elongation. The force on the nth lattice plane is due to the difference in the spring displacement just to the right of it with respect to the spring just to the left of it. If the value of the spring displacements can be obtained from

$\begin{array}{l} δ l_{i - 1} = l_{0} \frac{d u_{i - 1}}{d x} \\ δ l_{i} = l_{0} \frac{d u_{i}}{d x} \end{array}$

(1.24)

The difference of these spring displacements is:

$δ l_{i} - δ l_{i - 1} = l_{0} (\frac{d u_{i}}{d x} - \frac{d u_{i - 1}}{d x}) = l_{0}^{2} \frac{d^{2} u_{i}}{d x^{2}}$

(1.25)

where we've assumed that l₀ is small enough that we could use it to define the second derivative. The force on one nucleus in the nth lattice plane is then just

$F_{x} = (κ + 2 κ_{d} + 4 κ_{b d} / 3) l_{0}^{2} \frac{d^{2} u_{n}}{d x^{2}}$

(1.26)

where k is the spring constant. The acceleration of the mass, m, of each nucleus is then

$\frac{d^{2} u_{n}}{d t^{2}} = \frac{F_{x}}{m} = \frac{(κ + 2 κ_{d} + 4 κ_{b d} / 3)}{m} l_{0}^{2} \frac{d^{2} u_{n}}{d x^{2}}$

(1.27)

Equation (1.27) is the wave equation. It specifies a wave of speed

$c_{l o n g} = \sqrt{\frac{κ + 2 κ_{d} + 4 κ_{b d} / 3}{m} l_{0}^{2}}$

(1.28)

The wavelength, λ, of the wave will be a function of its wavelength, f (which is by the driving perturbation) as:

$λ_{l o n g} = \frac{c_{l o n g}}{f}$

(1.29)

The form of the wave is then:

$u (x, t) = A \cos (2 π (f t - \frac{x}{λ})) + B \sin (2 π (f t - \frac{x}{λ}))$

(1.30)

where A and B are constants determined by the driving conditions.

2. Transverse Wave Frequency

This analysis might be similar to the analysis of the wave speed and frequency of a pre-tensioned string. For the string, its vibration does not generally change the built-in tension so the solution for the frequency treats this pre-tension as a constant. However, for a solid at equilibrium, we don't generally have a large built-in tension between lattice planes. This leads, as we will show below, to amplitude-dependent wave parameters.

As depicted in Figure 3, for small slopes, du/dx<<1, we need to have an angle between the springs adjacent to the nth nucleus in order to have a net vertical force on the nucleus.

You need to realize that if du/dx is constant across the entire solid, this just represents a rotation about the z axis as shown in Figure 6 where no springs are either compressed or elongated.

Figure 6: A valid solid with constant du/dx. As you can see, constant du/dx result in a simple rotation of the solid.

One might at first think that a solid with all cells having the same du/dx with relative shear between the cells as shown in Figure 7 might be possible. However, the du/dx variation requires a discontinuity in u and that is not physical.

Figure 7: A system where all cells have a vertical shear of 0.3 radians. However, this is not possible since

it requires a non-physical discontinuity at the left-right cell boundaries.

From this discussion it should be obvious that the important parameter is the change in du/dx from lattice plane to lattice plane as shown in Figure 8 and that change is

${\frac{d u}{d x})}_{n} - {\frac{d u}{d x})}_{n - 1} = \frac{d^{2} u}{d x^{2}} l_{0}$ (1.31)

Figure 8: Two adjacent cells with different du/dx and therefore a non-zero d²u/dx².

The force on any lattice plane is, from the section on shear modulus:

$F = n_{z} n_{y} θ l (κ_{d} + 4 / 3 κ_{b d})$

(1.32)

where n_zn_y is the number of nuclei in that lattice plane. We need the difference in the force between those on the i-1 and i lattice planes to obtain the correct force on the ith plane:

$\begin{array}{l} δ F = n_{z} n_{y} l (κ_{d} + 4 / 3 κ_{b d}) \frac{d θ}{d x} = \\ n_{z} n_{y} l^{2} (κ_{d} + 4 / 3 κ_{b d}) \frac{d^{2} u}{d x^{2}} \end{array}$

(1.33)

We set δF equal to the mass, m, of the nuclei in the lattice plane, mn_yn_z, times the acceleration in the u direction:

$n_{y} n_{z} m \frac{d^{2} u}{d t^{2}} = n_{z} n_{y} l^{2} (κ_{d} + 4 / 3 κ_{b d}) \frac{d^{2} u}{d x^{2}}$

(1.34)

Equation (1.34) is the wave equation and the wave's speed is:

$c = \sqrt{\frac{(κ_{d} + 4 / 3 κ_{b d}) l^{2}}{m}}$

(1.35)

The wavelength of the wave depends on the speed and frequency, f:

$λ_{s h e a r} = \frac{c_{s h e a r}}{f}$

(1.36)