Electromagnetic
Introduction
This
animation shows the behavior of a bell propelled by two solenoids which have
oppositely flowing currents providing force to a magnet that is situated
between them. There are also two
restoring springs that bring the striker (gong) back to center when there is no
current flowing. For simplicity, it is
assumed that the driving frequency of the coils is much lower than the resonant
frequency associated with the spring constant, k, of the springs and the mass
of the gong although those effects, as well as drag of the gong slider bearings
could easily be incorporated.
Illustration with Captions
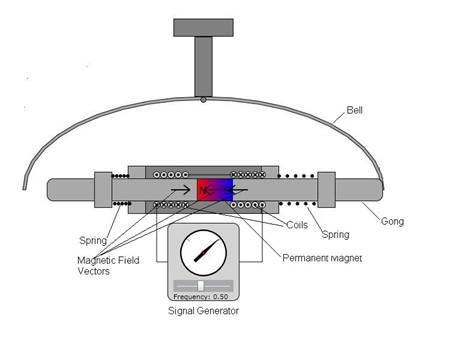
Figure 1: Diagram of a diametrical cross section of the
animated bell. Note the labels on the bell, the striker (or gong), the
centering springs, the Coils, and the permanent magnet (PM). Especially note that the magnetic field
vector of the left coil opposes (repels) that of the PM while that of the right coil is in the
same direction (attracts) as that of the PM.
These forces are consistent with the gong being displaced to the right
of center as shown. Note that the coil wire cross sections have either dots or
crosses inside. These symbols show the
direction of the current which for the cross is away from the observer (into
the screen) or toward the observer (coming out of the screen). The direction of
the magnetic field is determined by placing your right hand around the coil
such that your fingers are pointing in the direction of the current. Then, for the right hand coil, your fingers
would be directed into the screen and your thumb would be pointing in the
direction of that coil’s magnetic field which agrees with the arrow shown.
Physics
The physics of this device is quite simple. The coils create magnetic fields which change direction every half cycle. These magnetic fields interact with that of the permanent magnet (PM) such that one coil repels the PM and the other coil attracts the PM. This is usually termed push-pull operation.
To be more quantitative, we can estimate the force that moves the PM. The incremental force, dF, felt on each incremental length, dl, of the coil wire is given by:
(1)
where i is the current, F, dl, and B are vectors, B being the magnetic induction due to the PM, and the cross between dl and B denotes a cross product.
When the PM is coaxial with the coil, the current is along the f direction and the PM has radial component Br and axial component Bz so the components of the cross product are:
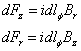(3)
Therefore it is the radial component of the PM field that is important for the axial force between the coil and the PM. Also, since Fr is either outward or inward for all f, there is no net radial force unless the axes of the PM and coil are misaligned. The total axial force on a solenoid (or, oppositely, on the PM) is given by the sum:
(4)
where Br n is the PM’s radial magnetic field at the nth turn and N is the total number of turns in the coil.
The radial field of a cylindrical PM close to the pole of the PM is outward for a North pole and inward for a South pole so that a South pole’s axial force on the same coil will be opposite that of a North pole’s axial force (as we learned in grade school). Its exact value is dependent on the PM’s residual flux density, which is the value of B inside a very large PM, as well on the radius and especially the axial length of the PM since a short PM’s South Pole tends to cancel the B field of the North pole.
The following .pdf file gives a very complete discussion of theory and experiment for the axial forces between cylindrical PMs of various lengths and very general solenoid designs.
http://sinantaifour.com/documents/papers/axial-force.pdf
The theory for algebraic results is very complicated but I have used Finite Element Analysis to compute the appropriate radial magnetic fields that the solenoid experiences and these are shown in Figures 2 and 3.
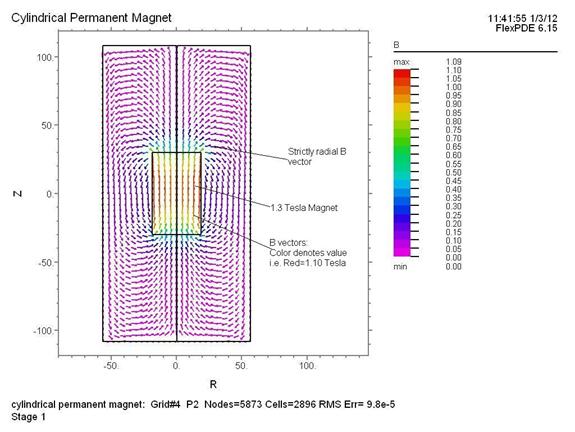
Figure 2:Vector B fields of a
Figure 3. Radial field of a
The above Figures assume a residual flux density, Bres of 1.3 Tesla. As can be observed in Figure 3, the resulting
radial flux density varies from about 0.23 Tesla at edge of the pole to near
zero at the top of the coil. The resulting axial force for a coil of radius 2.5
cm carrying a current of 1 amp, and a PM of length 6 cm and radius 1.9 cm is 0.089
Appendix
The information below is what I was able to find while
looking for information on the forces between a coil and a coaxial PM.
An equation that gives the axial force between 2 cylindrical PMs is:
where M is the magnetization of the PMs, R is their radius, L is their length, and z is their pole separation which must be at least as large as L for this equation to be valid. M is given in terms of the PM dipole moment, m, by the equation:
where V is the volume of the PM.
http://en.wikipedia.org/wiki/Electromagnet#How_the_iron_core_works
According to the site above the force between two axially aligned magnets and/or electromagnets is:
m1 and m2 are the magnetic moments of the magnets, r is the distance between the poles of the magnets and m0 is the permeability of vacuum. For the electromagnet the appropriate m value is given by:
where N is the number of turns (N=5 in Figure 1), i is the current, A is the axial area of the solenoid and L is the length of the solenoid. For the permanent magnet the site
http://www.kjmagnetics.com/specs.asp
shows that the residual flux density, Br, is about 1.3 Tesla measured in . That would result in a magnetic moment of
The ampere is defined such that the force
per unit length between 2 long
wires carrying 1 ampere separated by a distance, r, of 1 meter would experience
a force of 2x1-7
Then the force between 2 very short solenoids of radius rs and with a number of turns N separated along their axes by a distance much less than their length is:
