Ellipse on a Ramp

Introduction

The purpose of this animation is to show how to make an ellipse “roll” on a ramp. The term “roll” means that the point of contact of the exterior of the ellipse remains on the ramp. The point of contact is, of course, where the slope of the exterior of the ellipse equals the slope of the ramp. The problem here is to first find the point on the ellipse exterior that satisfies that condition and then to use that point to compute the new point where the center of the ellipse resides. The center point’s distance from the ramp varies as well its speed parallel to the ramp.

Calculations

The parametric equations for an ellipse are

where 2a is the width of the ellipse and 2b is the height of the ellipse and t varies from 0 to 2p.

To rotate the ellipse about its center (x,y)=(0,0) we multiply the above values by the 2x2 rotation matrix:

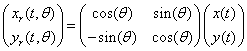
where this matrix results in the ellipse being rotated clockwise by angle q.

If now we want to find the x,y values where this rotated ellipse has slope dy_r/dx_r=s where s is the slope of the ramp, we just need to form this derivative using the chain rule thusly:

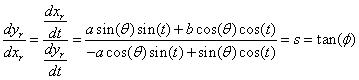
where f is the angle of the slope of the ramp. We can solve for the value t₀ where the above equation is satisfied and obtain:

However, we recognize the identity where the tangent terms of t₀ can be re-written:

Since the tangent of an angle is periodic with a period of p, we must modify the above equation so that all q+f are within the interval 0 to 2p:

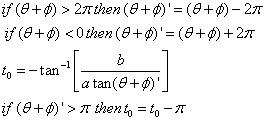
If we want to have the ellipse tangent to the line (where s is negative):

we shift the ellipse vertically by the following equation:

and continue to plot y_rs vs x_r(t,q);

If y(x) is more complex so that its x intercept is x=x₀, e,g,:

then the shifted y_rs becomes:

Now suppose that the axis of rotation of the ellipse is not (x,y)=(0,0) but instead

(x,y)=(x_c,y_u) and we still want to have it tangent to the ramp y(x). Then we have to use the following (x,y) values:

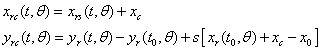
The y ordinate of the center will be at

In actual practice we let x_c advance as in the equation:

where the square root is recognized as the radius of the ellipse at the point of contact.