Evaporation and Condensation
Introduction
Evaporation and condensation are complex molecular phenomena. A good animation of these reversible processes is essential to their understanding. The animation discussed here will provide that understanding.
Figures
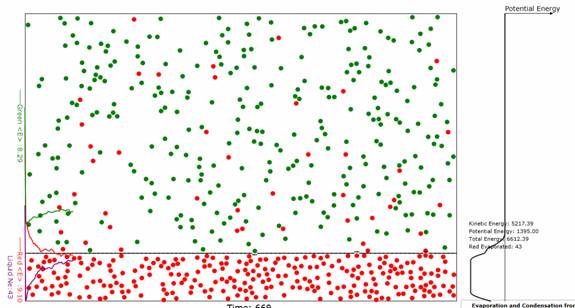
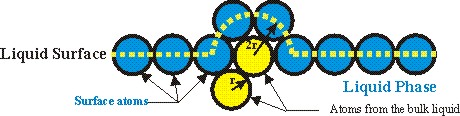
Figure 1: Showing surface barriers (potentials) and
liquid and gas phases
color coded to be red and green. Note that some of the red molecules have
evaporated (shown as red) into the vapor space and are therefore candidates for
re-deposition in the liquid.
Figure 2. Figure related to Reference 1 showing the the
heat of vaporization is a fairly simple function of the product of the surface
tension and the area of a displaced hemisphere through which the centers of
atoms pass at the surface of a liquid or solid.
Physics of Evaporation and Condensation[1]
All atoms or molecules have critical energies, Ee, above which they can exit the liquid or solid domain in which they are presently bound and enter the gas phase (evaporate) outside that domain. As shown in Reference 1, this energy is directly proportional to the surface tension (or, equivalently, the surface energy) of the surface of the particular liquid or solid in question (see Figure 3). Similarly all atoms or molecules in a gaseous state have critical energies, Ec, below which they may condense or dissolve into a neighboring liquid or solid surface or volume. Gaseous atoms with energy higher than Ec just reflect off the interface between the media. Since total energy in a closed system is conserved, the energy that a atom loses evaporating from the liquid or solid state is regained when it is condensed back into the liquid or solid state. In physics we call the energy needed for evaporation the potential barrier energy. An atom that has just been evaporated loses the potential barrier energy which is a substantial fraction of its kinetic energy while an atom that has just been condensed gains back a similar kinetic energy. So recently condensed atoms are "hot" but that extra kinetic energy is quickly dissipated via scattering with the cooler atoms of the liquid or solid. The animation permits adjustment of the potential energies as well as the average energies of the liquid, gas, and solid domains.
Evaporative Cooling
It's not so obvious from what has just been discussed, but when an atom has enough energy to evaporate, it carries a substantial fraction of its native media's energy with it. Since the atomic kinetic energy distribution is an exponential
![]()
and the total energy greater than Ec is given by ratio of the integrals:

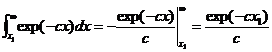
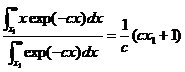
where c=1/kT and Ec =x1. Note that the average energy of the entire
energy range is kT.
Then only those atoms with E>Ec can evaporate, the change in average energy is:
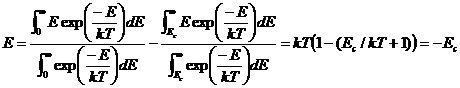
which is essentially the average energy of all the atoms with energy above Ed. Thus, on average, when an atom evaporates, it reduces the energy of the entire atomic ensemble by:
![]()
The total loss of energy when a large group, Ne, of atoms evaporates is of course
![]()
Solving for the final temperature, Tf, and taking the differential we have
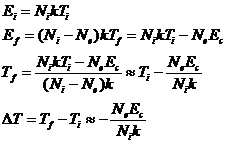
where the approximation is valid
when Ni>>Ne.
Another way of expressing this equation is to compute the heat energy of evaporation, Q, per gram molecular weight, n, evaporated:
![]()
where A is Avogadro's number.
Specifics of Evaporation and Condensation
The
ions have to have more than a certain critical energy climb the potential hill at
the surface of the solid and thereby to escape their host and become vapor
atoms. This is called the enthalpy of
evaporation. On the other hand, one
might think that
vapor atoms would always be re-deposited (condensed) back onto the liquid
surface since they only have to drop down the potential hill at its
surface. That concept, however, does not
take into account the fact that the vapor atom undergoes collisions with the atoms
at the surface of the Liquid. If the
kinetic energy of the vapor atoms is too large and/or the direction of the
nearest liquid atom is outward from the surface, the vapor atoms just recoil
from the surface rather than being deposited on it. These recoils are shown as part of the
animation.