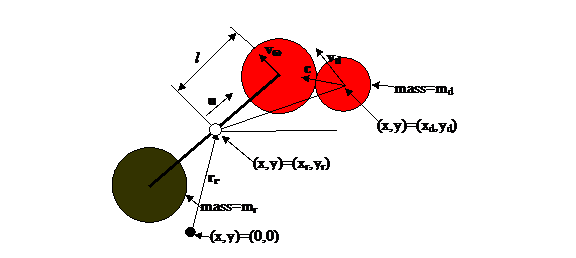Response of a 2D Fixed Rotor to a Disc Collision

Introduction

In order to simulate behavior of materials which have magnetic dipoles (modeled as rigid rotors) that are fixed in position inside, we need to compute the final rotor angular rotation rate after a collision with a disc as well as the final velocity of the disc. That calculation is performed in section 2. In section 1, as a warm up, the response of a rotor to a known impulse is computed.

1. Response of a Stationary Rotor to an Impulse Applied to One of Its End Masses

The basic driver involved in hard object collisions is an impulse. An impulse is the product of a force times a very small time increment which, of course, leads to a change in momentum like mδv where m is the mass and δv is the change in the velocity. The time increment is small enough that there will be no significant rotation of the rotor or displacement of its center of mass within the duration of the impulse. These motions will occur after the impulse.

The specific diagram for this problem is shown below. To make the problem primitive and simple, both of the initial motions are nil. The final motion will be a combination of a center of mass velocity, δv_x, and a final rotation, at rate δω, about the center of mass. The impulse is along the -x direction as shown.

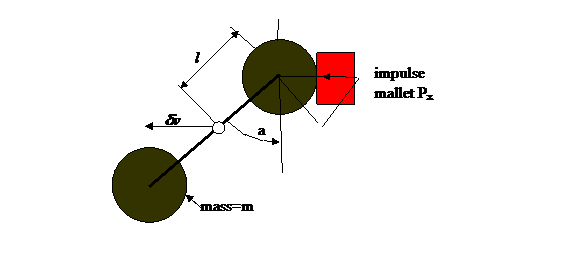
The rotor's rotation speed changes by δω. Here P_x is the impulse F_xdt; Note that P_x is negative:

$2 (m l δ ω \cos a) = P_{x}$

(1.1)

Solving for δω:

$δ ω = \frac{P_{x}}{2 m l \cos a}$

(1.2)

The energy supplied by the impulse is F_xdx which is the same as P_x<v_x> where <v_x> is the 1/2 of the final tangential speed that will be obtained by the rotor.

Thus conservation of energy requires that:

$m l^{2} δ ω^{2} = P_{x} \frac{l δ ω \cos a}{2}$

(1.3)

The solution for δω is:

$δ ω = P_{x} \frac{\cos a}{2 m l}$

(1.4)

2. Stationary Rotor-Disc Collisions

These are similar to hard disc collisions in terms of the momentum transfer. However, the initial and final velocities of each rotor end is a combination of the center of mass (CM) velocities and the rotational velocities. Therefore the momentum changes due to both of these incident velocities have to be equal and opposite to that of the disc and the total energy due to both types of rotor velocity as well as that of the disc has to be the same before and after the collision. For the time being we will limit ourselves to two dimensions (x,y). We can state the r and v vectors in terms of the (x,y) coordinate system and the z axis will be the rotation axis.

$\begin{array}{l} v_{p} = ω_{} l (- x \sin a_{} + y \cos a_{}) \\ v_{n} = - ω_{} l (- x \sin a_{} + y \cos a_{}) \end{array}$

(1.5)

where subscript p denotes one end (think positive) and n denotes the other end of the rotor, ω is the rotation speed of the rotor, l is half the distance between the rotor ends and a is the angle with respect to the x axis of the rotor's orientation. So the program must check the distances between both the p and the n ends of each rotor and the center of the disc. If this distance is less than or equal to the sum of the radius of the rotor end disc and that of the free disc, then a collision must be calculated. Just as in the case of the hard discs, the momentum transfers must be equal and opposite. However, unlike that case, the momentum transferred to the fixed rotor will be just its rotational speed changes.

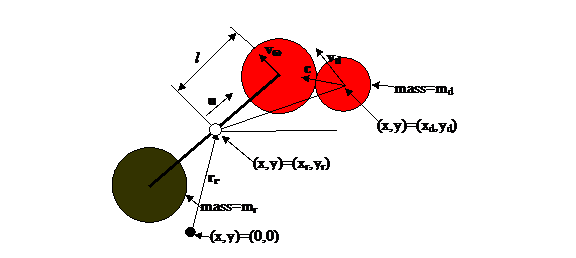
Figure 1: Illustration of rotor and a disc. The rotor rotational angle with respect to the x axis is a and rotor center of mass velocity v_r The distance between the centers of the rotor end discs is 2l and the radius of the end discs is b_r while the single disc radius is b_d Thus a collision is computed when the distance between disc center and either rotor end center is less than b_r+b_d. u is a unit vector along the length of the rotor, v_ω is a unit vector along the rotational velocity vector of the red end, and c is a unit vector along the line from the center of the disc to the red end of the rotor.

The impulse felt by the disc is along the central vector -c so its velocity change will be along that direction also and we will assign the value δv to the magnitude of that velocity change. This results in a new value of kinetic energy of the disc:

$E_{d}^{'} = \frac{m_{d}}{2} (v_{d} - δ v c) • (v_{d} - δ v c) = \frac{m_{d}}{2} (v_{d}^{2} + δ v^{2} - 2 δ v c • v_{d})$

(1.6)

as well as a new momentum

$p' = m_{d} (v_{d} - δ v c)$

(1.7)

In the collision, linear momentum is not conserved because the rotor center is fixed but angular momentum about the center (rotation axis) of the rotor does have to be conserved. The initial angular momentum of the disc is

$L_{d} = m_{d} [l u - (r_{r} + r_{d}) c] \times v_{d}$

(1.8)

and the initial angular momentum of the rotor is

$L_{r} = 2 m_{r} l^{2} ω$

(1.9)

and of course both of these angular momenta are along the z direction. The angular momentum of the disc gets changed to

$L_{d} = m_{d} [l u - (r_{r} + r_{d}) c] \times (v_{d} - δ v c) = m_{d} [l u - (r_{r} + r_{d}) c] \times v_{d} - m_{d} l δ v (u \times c)$

(1.10)

and the angular momentum of the rotor becomes:

$L_{r}^{'} = 2 m_{r} l^{2} (ω + δ ω)$

(1.11)

The total angular momentum after the collision must be equal to that before the collision and therefore :

$- m_{d} l δ v (u \times c) = 2 m_{r} l^{2} δ ω$

(1.12)

The total change in kinetic energy of the disc and rotor has to equal zero and therefore we have

$\frac{m_{d}}{2} (v_{d}^{2} + δ v^{2} - 2 δ v c • v_{d}) + m_{r} l^{2} {(ω + δ ω)}^{2} = \frac{m_{d}}{2} v_{d}^{2} + m_{r} l^{2} ω^{2}$

(1.13)

We can solve equations (1.12) and (1.13) for both δω and δv. First simplifying the notation for δω we have:

$\begin{array}{l} δ ω = - \frac{m_{d} l δ v (u \times c)}{2 m_{r} l^{2}} \equiv a δ v \\ a = - \frac{m_{d} (u \times c)}{2 m_{r} l} \end{array}$

(1.14)

In the next 4 lines we solve for δv

$\begin{array}{l} \frac{m_{d}}{2} [δ v^{2} - 2 δ v c • v_{d}] + m_{r} l^{2} (2 ω δ ω + δ ω_{}^{2}) = 0 \\ \frac{m_{d}}{2} [δ v^{2} - 2 δ v c • v_{d}] + m_{r} l^{2} (a^{2} δ v^{2} + 2 ω a δ v) = 0 \\ δ v^{2} (\frac{m_{d}}{2} + m_{r} l^{2} a^{2}) + δ v (2 m_{r} l^{2} ω a - \frac{m_{d}}{2} 2 c • v_{d}) = 0 \\ δ v = - \frac{(2 m_{r} l^{2} ω a - m_{d} c • v_{d})}{(\frac{m_{d}}{2} + m_{r} l^{2} a^{2})} \end{array}$

(1.15)

and then we can insert the value of a and solve for δω:

$\begin{array}{l} δ ω = - a \frac{(2 m_{r} l^{2} ω a - m_{d} c • v_{d})}{(\frac{m_{d}}{2} + m_{r} l^{2} a^{2})} \\ a = - \frac{m_{d} (u \times c)}{2 m_{r} l} \\ δ ω = \frac{m_{d} (u \times c)}{2 m_{r} l} \frac{(- l^{} ω (u \times c) - c • v_{d})}{(\frac{1}{2} + \frac{m_{d}^{}}{m_{r}} {(u \times c)}^{2})} \end{array}$

(1.16)

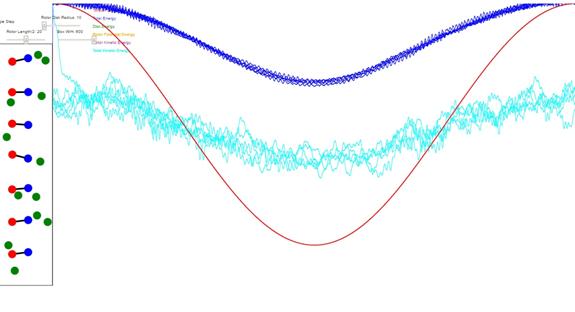
Figure 1: Results of a 2D animation of a magnetization cycle. Red is the magnetic field, blue is the total energy including magnetic potential energy, and cyan is the kinetic energy. While the magnetic field is high, kinetic energy can be reduced by cooling gases outside the container. When the magnetic field is reduced, the kinetic energy is reduced and the container is placed in thermal contact with the volume which is desired to be cooled.