Forced Harmonic Oscillator Motion
Introduction
The forced simple harmonic oscillator’s (FSHO) motion is a good approximation of the driven motion of practically all real-world objects that present periodic motion. Even though the FSHO’s restoring force is linear in displacement, its motion is a good approximation for a motion of a system with non-linear restoring force, at least within a limited range of the latter’s displacement. Therefore a good grasp on the dynamics of the FSHO goes a long way toward understanding the dynamics of the real world.
Calculations:
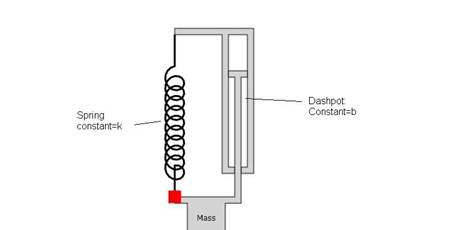
Figure 1: The oscillator showing the spring, the
dashpot and the mass.
The picture above shows the
important parameters of the FSHO. They include a spring (shown here as a coil
with spring constant k
The equation that describes the motion of the mass is:
![]() (1)
(1)
where F0 is the peak
force and w is the radian frequency of
that force.
To solve equation 1 we make the substitution:
![]() (2)
(2)
where i is the square root of -1, Real[] denotes the real part of the resulting value, Y is the complex peak displacement for the given force, t is time, and wc (which has units of 1/time and is complex) is a parameter for which we will solve.
Using equation 2 in equation 1 we have very easily:
![]() (3)
(3)
The result for Y is:
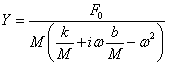 (4)
(4)
For convenience we make the following definitions:
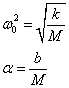 (5)
(5)
so that equation 4 becomes.
 (4a)
(4a)
Also, we now separate the real and imaginary parts of equation 4a by re-naming these quantities:
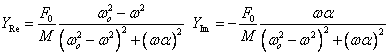 (6)
(6)
First, notice that the real part of YRe
is positive when w<w0 and
negative when w>w0. Also note that YIm
is always negative.
Using equations 6 in equation 2 we have
![]() (7)
(7)
We may use trigonometric identities to show the phase lag of equation 7:
![]() (8)
(8)
where the function atan2(y,x) obtains the arctangent of y and x on the range – p to p.
Note that the phase in equation 8 always negative (a phase
lag) and its magnitude is less than p/2
when w<w0 and greater
than p/2 when w>w0
and goes to p as w goes to infinity.
The coil and magnet force inducer
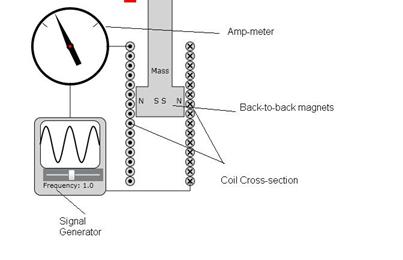
Figure 2: elements involved in inducing the force on
the mass of the oscillator.
The goal of the forcing element is to avoid any physical contact with the mass. That is achieved using an external coil and a pair of bar magnets which is poled so that both the left side and the right side of the pair have a North pole pointing outward toward the wires. Then the current shown in the coil cross section alternately applies upward and downward forces on the magnet depending on the direction of current from the signal generator. Since the magnet’s response is a reaction to the forces felt by the fixed wires, the direction of these forces are opposite to the ones that are felt by the wires.
The frequency available from the signal generator is
variable as can be seen by the speed of progress of the Force and Displacement
plots.
Summary
Equations 6, 7, and 8 are probably the most important
equations in the real world for understanding driven periodic motion. The animation accompanying this document will
help you to fully appreciate these equations.