Casino Gambling

Introduction

            The purpose of this animation is to show the learner that all gambling by Casino rules is ultimately futile.  The real reason is that the Casino has essentially infinite financial backing and the gambler's financial backing is very limited.  So the gambler will always run out of money unless he quits before that happens.  But, even if he quits while he is still either ahead or solvent, the rules of chance say that when he returns with what he had on the previous gambit, he will eventually lose his money.

            For this animation, we'll assume very simple gambling rules.  Initially we'll assume that the betting is like making a single coil toss.  If the bettor bets heads, for example, and heads comes up he wins his bet, otherwise he loses his bet.  This, of course is not acceptable for the Casino so we will provide the option of a coin with a slight weight bias that provides a small advantage to the Casino.  We can call the small advantage the Casino payout which will be less than 100%.  If, for example, the payout is 90%, that means that if the gambler has a total cash flow of $10,000 (the sum of all the bets he has made), after many, many very small bets, he can expect to have won back $9,000 and have lost $10,000 for a net loss of $1000.  In other words, he wins 45% of his bets and the casino wins 55% of its bets.  

 

            For small bets, the starting cash that the gambler would expect to need in order to have a mean total cash flow of $2,000 would be about $200.  Let's assume that the bet size is always $10.  The minimum number of bets to lose all his money is obviously 20.  The maximum number of bets before folding tends toward infinity but these cases have a very small probability.  The actual history of his total cash is like a bell curve that has a lower limit of zero and a center value of about $200.  This, of course, is a distorted bell curve.  The more bets that are made before folding, the wider the bell curve becomes.  If the Casino allowed the bettor to go into debt, then the bell curve would be symmetrical centered around the bettor's original cash.

 

Math

            Let's take an actual gambling device, the American roulette wheel.  This has 38 slots supposedly equally weighted.  Eighteen are painted red and these belong to the bettor.  The other 20 are painted black and these belong to the Casino.  The percent payback is calculated with the following equation:

p=100( 18 38 − 20 38 )=5.26% MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadchacqGH9a qpcaaIXaGaaGimaiaaicdadaqadaqaamaalaaabaGaaGymaiaaiIda aeaacaaIZaGaaGioaaaacqGHsisldaWcaaqaaiaaikdacaaIWaaaba GaaG4maiaaiIdaaaaacaGLOaGaayzkaaGaeyypa0JaaGynaiaac6ca caaIYaGaaGOnaiaacwcaaaa@4738@  

(1.1)

 

Thus the house has an approximate 5.3% advantage on the bettor and the house payback is about 94.7%.  The bettor can gamble each dollar about 20 times before expecting to lose so his cash flow would be approximately 20 times his starting cash. 

 

            What makes gambling so appealing is that the bettor can easily find himself beating the Casino for significant periods of time.  For this case, the laws of probability say that he can reasonably expect to quite often win up to approximately the square root of 20 (4 or 5 times) keeping the same bet size.  But the more times he bets, the greater the effect of the Casino's 5.26% advantage has on his money.  The losses due to this advantage are directly proportional to the number of bets he makes while the gains he makes by chance are proportional only to the square root of his number of bets.

Figures

In this animation, I have included 3 types of plot. 

First I show the history of a single starting bet Vs time.  This is really what is called a random walk plot but its lower limit is zero.

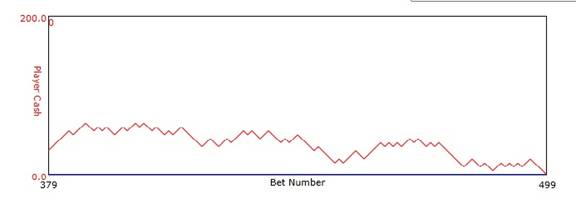
Figure 1:  Plot of player cash Vs bet number.  Player's starting cash was $100 and bet size was $5.  House advantage was 2%.  The player folded after 500 bets.

 

In addition I show a plot of the results of many, many bettors each starting with a fixed amount of cash and betting a small fraction of the cash until all their cash is gone (i.e. they have folded).

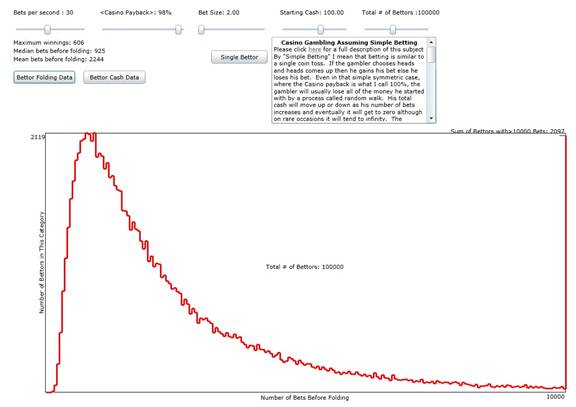
Figure 2: The number of bettors (out of a total of 100,000) Vs the number of bets before folding.  The parameters are the same as Figure 1 except the bet size has been reduced to $2.

 

Also, for the same set of folding bettors as the previous paragraph, I show a plot of the total bettors' cash in cash categories ranging from zero to the maximum winnings at any one time. 

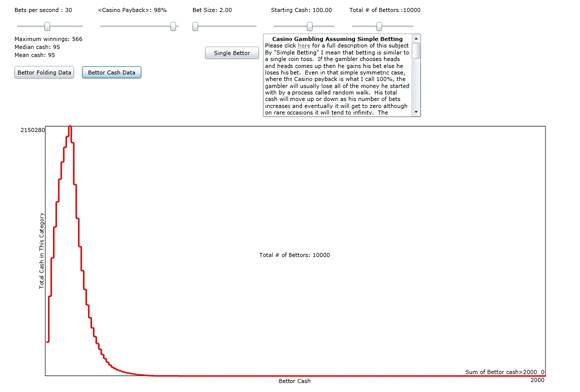
Figure 3:  A history total cash for all players Vs the cash category.  The parameters here are the same as in Figure 2 except here the total number of bettors are 10,000.