Gas Centrifuge

Introduction

The gas centrifuge provides a good framework for learning Newtonian and thermal physics of a large ensemble of particles (usually molecules or atoms). In this document I will first give the standard macroscopic Boltzmann treatment of the radial distribution of particles of different mass. Then I will document on a more microscopic basis the dynamics of how the radial distribution is achieved. Finally I show the mathematics of the velocity changes when two particles of different mass and arbitrary velocities collide.

Figures

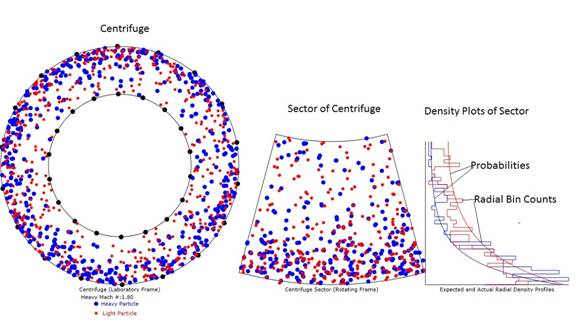
Figure 1: Diagram of the animation with heavy particle speed at Mach 1.8. Note that the particle density is much more dense at the outer radius than the inner radius. Also note that the radial probabilities and radial bin counts are reasonably well matched except for the expected variances due to only 600 particles and therefore an average of only 1 particles in each of the 40 bins polled.

Average Radial Particle Distribution in an Artificial Gravity

1. Standard Thermal Physics Treatment

The Boltzmann probability law for particle height, in a gravity (or acceleration field), g, is:

$P (h) = N \exp (\frac{- m g h}{k T})$ (1)

where N is a normalization constant, m is the mass of the particle, k is Boltzmann's constant, h is the height of the particle with respect to the center of the gravitational field, and T is absolute temperature. It will be adequate to model g as

$g = - ω^{2} r$ (2)

where ω is the rate of rotation (radians per second) and r is somewhere between the inner radius, r_I, and outer radius, r_O . Note that the sign of g is negative since the acceleration is toward the axis of the centrifuge.

Then equation 1 becomes

$P (m, r) = N \exp (\frac{m ω^{2} r^{2}}{k T})$ (3)

Equation 3 is the time-averaged particle density Vs mass and radius distribution in the annulus of the centrifuge. Note that the quantity in the numerator of the exponent of equation 3 is just mv_t²(r) where v_t(r)is the average tangential speed of the particle. The speed of sound in an ideal gas is:

$v_{s} = \sqrt{\frac{γ k T}{m}}$

where γ is the ratio of specific heat at constant pressure to that at constant volume and is usually of order unity (for air γ=7/5). Thus equation 3 can be converted to the simpler form:

$P (m, r) = N \exp (γ \frac{m v_{t}^{2} (r)}{m v_{s}^{2}}) = N \exp (γ M_{m}^{2} (r))$ (3a)

where M_m=v_t/v_s is the Mach number associated with the particular gas. Note that the heavier gas will have a lower Mach number than the lighter gas. Also note that the movement of the gas from being uniformly distributed to being higher density at the outer radius of the centrifuge doesn't become significant at Mach numbers less than about1.0.

2. Microscopic Treatment

a. Providing Centripetal Acceleration

Equations 3 are just formalisms and don't explain on a microscopic basis how this radial distribution is achieved and maintained. It is clear that the centripetal force needed to keep individual particles rotating in an approximate circle about the axis of the centrifuge has to come from their collisions with the outer boundary. Obviously the average rate of radial momentum transfer must be sufficient to provide the acceleration described in equation 2:

$〈 {(\frac{d p_{r}}{d t})}_{O} 〉 = - m ω^{2} < r >$ (4)

where <r> represents the average value of r. If wall collisions are separated in time by a representative time, τ, then we can say that for any one collision we must have:

$Δ p_{O} = m ω^{2} < r > τ$ (5)

and the difference in the radial speed changes is:

$Δ v_{O} = ω^{2} < r > τ$ (6)

Equation 6 seems to be independent of the mass of the atoms but doesn't take into account the difference in thermal speeds between atoms of different mass. Since the less massive atoms move faster, they will collide more times per second with the outer wall and gain more inward speed.

The number of wall collisions per second per wall unit area is

$\frac{d n}{d t} = n < v_{t h} >$ (7)

where n is the number of molecules per unit volume and <v_th> is the average thermal velocity of the molecules. In order to keep the entire volume, V, of the gas moving in a circle, the inward momentum supplied by the entire area, A, of the outer boundary is

$\frac{d N}{d t} = 2 n π (r_{O} + r_{I}) L < v_{t h} >$

$Δ p \frac{d N}{d t} = n V m ω^{2} < r > = π n L (r_{o}^{2} - r_{I}^{2}) m ω^{2} < r >$

$Δ p = \frac{m ω^{2} < r > (r_{O}^{2} - r_{I}^{2})}{2 (r_{O} + r_{I}) < v_{t h} >} = \frac{m ω^{2} < r > (r_{O}^{} - r_{I}^{})}{2 < v_{t h} >}$ (8)

where Δp is the average momentum provided per collision, r_O is the outer radius and r_I is the inner radius and <r> is the mean radial location of the molecules. If the axial length of the centrifuge is L then:

$\begin{array}{l} A = 2 π r_{O} L \\ V = π L (r_{O}^{2} - r_{I}^{2}) \end{array}$ (9)

When equations 7 and 9 are inserted into equation 8 we have:

$2 n Δ p π r_{O} L < v_{t h} > = π n L (r_{O}^{2} - r_{I}^{2}) m ω^{2} < r >$ (10)

Solving equation 10 for Δp we have:

$Δ p = \frac{(r_{O}^{2} - r_{I}^{2}) m ω^{2} < r >}{2 r_{O} < v_{t h} >}$ (11)

For low Mach numbers we can assume that <r>=(r_O+r_I)/2 and we know from thermal physics that

$< v_{t h} > = \sqrt{\frac{k T}{m}}$ (12)

so that equation 11 becomes:

$Δ p = \frac{(r_{O}^{} - r_{I}^{}) m ω^{2} < r >^{2}}{2 r_{O} < v_{t h} >} = \frac{(r_{O}^{} - r_{I}^{}) m < v_{t} >^{2}}{2 r_{O} < v_{t h} >}$ (13)

where v_t is the average tangential speed due to the centrifuge rotation and v_th is the average thermal speed. Dividing both sides of equation 13 by m we get the inward speed change Δv needed at each outer wall collision to keep the gas moving in a circle:

$Δ v = \frac{(r_{O}^{} - r_{I}^{}) < v_{t} >^{2}}{2 r_{O} < v_{t h} >}$ (14)

Note that equation 14 has units of speed as it must.

b. Bringing Particles up to the Tangential Speed of the Centrifuge

The previous section computes the inward radial speed increments needed for each wall collision in order to keep the molecules moving in approximate circles about the centrifuge axis. This section will deal with accelerating the gas so that it finally has the same rotational speed as the centrifuge. It's clear that inelastic collisions with the walls of the centrifuge are the only way that the gas can be accelerated. In order for the entire gas to be accelerated tangentially at rate α=dω/dt, we must have a certain change in angular momentum, ΔP, at each collision. The angular momentum equation is:

$\frac{d P}{d t} = I α = M < r >^{2} α = n π L (r_{O}^{2} - r_{I}^{2}) m < r >^{2} α$

where the moment of inertia, I, is implicitly defined as the total gas mass times the average radius squared. Following the previous section we have the total number of wall collisions per second as:

$\frac{d N}{d t} = 2 n π (r_{O} + r_{I}) L < v_{t h} >$

dividing the two equations we obtain

$\frac{d P}{d N} = \frac{n π L (r_{O}^{2} - r_{I}^{2}) m < r >^{2} α}{2 n π L (r_{O} + r_{I}) < v_{t h} >} = \frac{(r_{O}^{2} - r_{I}^{2}) m < r >^{2} α}{2 (r_{O} + r_{I}) < v_{t h} >} = \frac{(r_{O}^{} - r_{I}^{}) m < r >^{2} α}{2 < v_{t h} >}$

The tangential speed change for each collision can be computed from the following equation:

$\begin{array}{l} m Δ v r = Δ P o r : \\ Δ v = \frac{Δ P}{m r} \end{array}$

so that

$< Δ v_{t} > = \frac{(r_{O}^{} - r_{I}^{}) < r >^{} α}{2 < v_{t h} >}$

The way that the tangential speed is implemented in the program is to add the value

$δ v_{t} = ω r - v_{t}$

to the tangential speed at each inner or outer wall collision. Using this expression, the tangential speed of the atoms exponentially approaches the tangential speed of the outer wall of the centrifuge.

Particle-Particle Collisions of Different Mass or Velocity

Here we will consider spherical particles which have the different masses, m₁ and m₂, and diameter, D. The centers of the spheres will be labeled (x₁,y₁) and (x₂,y₂). Upon collision, the momentum transferred between the spheres will always be along the unit vector:

$u = \frac{[(x_{1} - x_{2}) \hat{x} + (y_{1} - y_{2}) \hat{y}]}{r_{12}}$ (19)

where

$r_{12} = \sqrt{{(x_{1} - x_{2})}^{2} + {(y_{1} - y_{2})}^{2}}$

is the distance between centers. Since the animation is illustrated in only 2 dimensions, we will simplify the analysis by doing it in 2 dimensions. The vector analysis in 3 dimensions is entirely similar except all velocities and positions have a z component.

The expression for the final momenta in terms of the initial momenta is:

$m_{1} v_{1}^{'} + m_{2} v_{2}^{'} = m_{1} v_{1}^{} + m_{2} v_{2}^{}$ (20)

where the apostrophe on the left side of the equations indicates the final velocities. We know that the energies are conserved so

$\frac{m_{1} v_{1}^{' 2} + m_{2} v_{2}^{' 2}}{2} = \frac{m_{1} v_{1}^{2} + m_{1} v_{2}^{2}}{2}$ (21)

The directions of the change in momenta are along the vector of centers, u, and the values of the changes of momenta must be equal and opposite.

$m_{1} Δ v_{1} = M δ v u = - m_{2} Δ v_{2}$ (22)

so that

$\begin{array}{l} m_{1} v_{1}^{'} = m_{1} v_{1}^{} + M δ v u \\ m_{2} v_{2}^{'} = m_{2} v_{2}^{} - M δ v u \end{array}$ (23)

Now we can use equation 23 in equation 21 to solve for the value of Mδv.

$\frac{(m_{1} v_{1}^{} + M δ v u) • (m_{1} v_{1}^{} + M δ v u)}{2 m_{1}} + \frac{(m_{2} v_{2}^{} - M δ v u) • (m_{2} v_{2}^{} - M δ v u)}{2 m_{2}} = \frac{m_{1} v_{1}^{2} + m_{2} v_{2}^{2}}{2}$ (24)

where the large dot stands for the dot product and equation 24 simplifies to:

$\begin{array}{l} \frac{(2 m_{1} M δ v u • v_{1}^{} + M^{2} δ v^{2})}{2 m_{1}} + \frac{(- 2 m_{2} M δ v u • v_{2}^{} + M^{2} δ v^{2})}{2 m_{2}} = 0 \\ M^{2} δ v^{2} (\frac{1}{m_{1}} + \frac{1}{m_{2}}) + 2 δ v M (u • v_{1}^{} - u • v_{2}^{}) = 0 \\ M δ v = \frac{2 m_{1} m_{2} u • (v_{2}^{} - v_{1}^{})}{m_{1} + m_{2}} \end{array}$ (25)

where we make the identification:

$M = \frac{2 m_{1} m_{2}}{m_{1} + m_{2}}$

and M is known as the "reduced mass".

Equations 23 and 25 are a complete solution for the final momenta. The final velocities are computed by dividing both sides of equations 23 by their respective masses:

$\begin{array}{l} v_{1}^{'} = v_{1}^{} + \frac{2 m_{2}}{m_{1} + m_{2}} u • (v_{2}^{} - v_{1}^{}) u \\ v_{2}^{'} = v_{2}^{} - \frac{2 m_{1}}{m_{1} + m_{2}} u • (v_{2}^{} - v_{1}^{}) u \end{array}$

Suppose m₂>m₁. Then we see that the magnitude of the speed added to molecule 1 will be larger than the magnitude of the speed removed from molecule 2. We can easily see from equation 24 that, even though the averages of the dot products are zero, that the collision results in an increased kinetic energy for molecule 1 and a decreased kinetic energy for molecule 2 because of the mass term in the denominators.

If the initial speeds are the same then the only difference between E₁ and E₂ is due to the M² term in the kinetic energies.

$Δ E_{1} - Δ E_{2} = M^{2} δ v^{2} (\frac{1}{2 m_{1}} - \frac{1}{2 m_{2}}) > 0$

If the speeds are different, say v₂>v₁, but the masses are the same, then the difference in kinetic energies is due to the Mm term in the kinetic energies:

$Δ E_{1} - Δ E_{2} = \frac{m}{2} [u • (v_{2} - v_{1}) u • (v_{1} + v_{2})] = \frac{m}{2} [{(u • v_{2})}^{2} - {(u • v_{1})}^{2}]$

The above equation can be re-written:

$Δ E_{1} - Δ E_{2} = \frac{m}{2} [v_{2}^{2} \cos^{2} (θ_{u 2}) - v_{1}^{2} \cos^{2} (θ_{u 1})]$

where

$\cos (θ_{u i}) = \frac{u • v_{i}}{v_{i}}$

is the cosine of the angle between v_i and u. The average value over all possible angles between v_i and u of the cosine squared terms is 1/2 so we can write

$< Δ E_{1} - Δ E_{2} > = \frac{m}{4} [v_{2}^{2} - v_{1}^{2}]$

Therefore, averaged over all possible angles between u and v, the change of kinetic energy for particle 1 will be positive since v₂>v₁.

This degradation of the energy of the larger mass or higher speed atoms and/or speed leads to what is called the zeroth law of thermodynamics-all energies tend to be become equalized because of collisions. An example of this would be two gases of different molecular masses as well as different temperatures injected into an insulated box. The gas temperatures (or average energies) will equalize leaving the average speed of the gas with more massive molecules less than that of the gas with less massive molecules but the energies will tend to become equal due to the energy Vs velocity law we just proved.

Let's compute the E₁and E₂ for the general case where both m and v are different.

$\begin{array}{l} E_{1}' = \frac{(m_{1} v_{1}^{} + M δ v u) • (m_{1} v_{1}^{} + M δ v u)}{2 m_{1}} = E_{1} + M δ v (u • v_{1}) + \frac{M^{2} δ v^{2}}{2 m_{1}} \\ E_{2}' = \frac{(m_{2} v_{2}^{} - M δ v u) • (m_{2} v_{2}^{} - M δ v u)}{2 m_{2}} = E_{2} - M δ v (u • v_{2}) + \frac{M^{2} δ v^{2}}{2 m_{2}} \end{array}$

Inserting the expression for Mδv we have:

$\begin{array}{l} E_{1}' = E_{1} + M u • (v_{2}^{} - v_{1}^{}) (u • v_{1}) + \frac{M^{2} δ v^{2}}{2 m_{1}} = E_{1} + M [(u • v_{2}^{}) (u • v_{1}^{}) - (^{u • v_{1}^{}) 2}] + \frac{M^{2} δ v^{2}}{2 m_{1}} \\ E_{2}' = E_{2} - M u • (v_{2}^{} - v_{1}^{}) (u • v_{2}) + \frac{M^{2} δ v^{2}}{2 m_{2}} = E_{2} - M [(^{u • v_{2}^{}) 2} - (u • v_{1}^{}) (u • v_{2}^{})] + \frac{M^{2} δ v^{2}}{2 m_{2}} \end{array}$

$\begin{array}{l} E_{1}' = E_{1} + M [(u • {\hat{v}}_{2}^{}) (u • {\hat{v}}_{1}^{}) v_{1} v_{2} - (^{u • {\hat{v}}_{1}^{}) 2} v_{1}^{2}] + \frac{M^{2} [v_{2}^{2} {(u • {\hat{v}}_{2}^{})}^{2} - 2 v_{1} v_{2} (u • {\hat{v}}_{2}^{}) (u • {\hat{v}}_{2}^{}) + v_{1}^{2} {(u • {\hat{v}}_{2}^{})}^{2}]}{2 m_{1}} \\ E_{2}' = E_{2} - M [(^{u • {\hat{v}}_{2}^{}) 2} v_{2}^{2} - (u • {\hat{v}}_{1}^{}) (u • {\hat{v}}_{2}^{}) v_{1} v_{2}] + \frac{M^{2} [v_{2}^{2} {(u • {\hat{v}}_{2}^{})}^{2} - 2 v_{1} v_{2} (u • {\hat{v}}_{2}^{}) (u • {\hat{v}}_{2}^{}) + v_{1}^{2} {(u • {\hat{v}}_{1}^{})}^{2}]}{2 m_{2}} \end{array}$

It's clear that, over many collisions, the (u.v₁)(u.v₂) terms average to zero.

Since the animation is digital we can expect that most often the collision condition will be realized when the distance between the centers of the two spheres,r₁₂, is less than D. To handle this I will increase the distance between the centers by the difference

$d r = D - r_{12}$

by shifting each sphere in opposite directions by dr/2 along u. Thus we will move the centers by the vectors:

$δ r_{1, 2} = \pm \frac{d r}{2} u$ (26)