Gas Expansion into a Vacuum Environment

Introduction

This animation considers the energy and pressure of a gas that is expanding due to the motion of one of the walls of its container. For this case I will assume that the wall is moving uniformly so as to increase the volume accessible to the gas and that the wall does not experience any retarding force because of any external gas pressure. This is in some ways more complicated than the usual gas physics situations where, for example, the gas expands while the pressure remain constant.

Figures

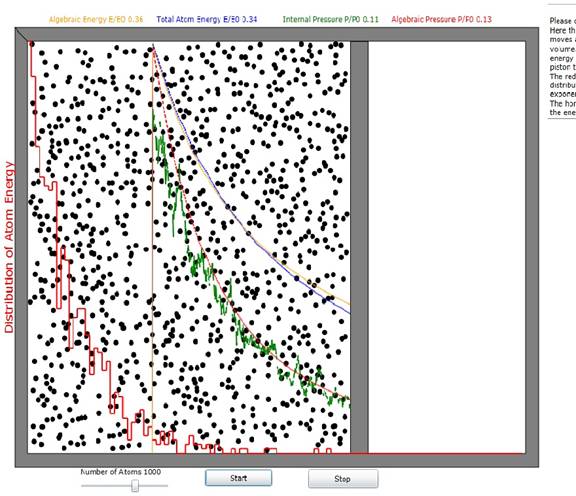
Figure 1: Gas expansion apparatus diagram. The moving wall (piston) starts at the location of the vertical orange line and moves to the right end of the chamber. Energy and pressure are plotted in blue and green, respectively.

Physics and Math

Since the wall moves away from the occupied volume, the gas atoms lose momentum and kinetic energy when hitting it. As a result of the energy reduction they impact all of the walls with less momentum and the pressure is reduced.

In the reference frame of the piston, the momentum change can be written:

$\begin{array}{l} δ p_{p} = - 2 m (v_{x} - v_{p}) L e a d i n g t o : \\ p_{p}' = m (v_{x} - v_{p}) - 2 m (v_{x} - v_{p}) \end{array}$

(1.1)

where the prime on p_p indicates the value of momentum after the collision.

In the laboratory reference frame:

$p'_{L a b} = m v_{p} - m (v_{x} - v_{p}) = m (2 v_{p} - v_{x})$

(1.2)

which results in the following energy change:

$E' - E = \frac{m}{2} [{(2 v_{p} - v_{x})}^{2} - v_{x}^{2}] = \frac{m}{2} (4 v_{p}^{2} - 4 v_{p} v_{x})$

(1.3)

Obviously v_x>v_p if the atom is to hit the piston. When v_x=v_p + δv_x then becomes

$δ E = - 2 m v_{p} δ v_{x}$

(1.4)

regardless of the magnitude of δv_x.

For an atomic area of x_p*h, where h is the piston height, the number of piston hits per second expected is

$\frac{d n}{d t} \approx \frac{1}{x_{p} h} (< v_{x} > - v_{p}) h = \frac{1}{x_{P}} (< v_{x} > - v_{p})$

(1.5)

where x_p is the length of the cylinder and h is the height of the piston.

Thus, combining equations (1.4) and (1.5), the expected energy loss per second is

$\frac{d E}{d t} = - 2 m v_{p} \frac{1}{x_{p}} {(< v_{x} > - v_{p})}^{2}$

(1.6)

When v_x is about equal to v_p then v_x doesn't change much nor does energy. Now we must consider another question: how to compute a meaningful value for <v_x> where only

<v_x> is greater than v_p is meaningful. That involves integrals over the Maxwell distributions:

$< v_{x} > = \frac{\int_{v_{p}}^{\infty} v_{x} \exp (- \frac{v_{x}^{2}}{v^{2}}) d v_{x}}{\int_{v_{p}}^{\infty} \exp (- \frac{v_{x}^{2}}{v^{2}}) d v_{x}} = \frac{< v_{}^{2} > {\exp (- \frac{v_{x}^{2}}{< v_{}^{2} >}) |}^{\infty}_{v_{p}}}{\sqrt{< v^{2} >} [1 - e r f (\frac{v_{p}^{2}}{< v_{}^{2} >})]}$

(1.7)

Converting equation (1.7) to average energy terms <E>=m<v_x²> we have:

$\frac{d < E >}{d t} = - 2 m v_{p} \frac{1}{x_{p}} {[\frac{\sqrt{\frac{2 < E >}{m π}} \exp (- \frac{m v_{p}^{2}}{< E >})}{1 - e r f (\frac{v_{p}^{2}}{E})} - v_{p}]}^{2}$

(1.8)

Now v_pdt=δx_p so we have the following differential equation which can only be solved iteratively:

$δ < E > = - 2 m {[\frac{1}{2} \sqrt{\frac{< E >}{π m}} \exp (- \frac{m v_{p}^{2}}{< E >}) - v_{p}]}^{2} \frac{δ x_{p}}{x_{p}}$

(1.9)

It turns out the that exponential value for the piston speeds used in the program is very close to 1.0 so the program uses the value

$\frac{δ E}{δ x_{b}} = 2 v_{p} < v_{x} > (< v_{x} > - v_{p}) / x_{p}$

(1.10)

Appendix: Rate of wall hits

Assuming that the container dimensions are much greater that the mean free path, l, we have the following cases:

1. If the distance of the atom from the wall is equal to l, then the probability that the atom hits the wall in l/v_x seconds is 0.5.

2. If the distance of the atom from the wall is equal to fl, then the probability that the atom hits the wall in l/v_x seconds is 0.5/f².

There are N(fl/x_P) atoms within nl of the piston.

Converting statement 2 into an equation we have:

$\begin{array}{l} P (f) = \frac{0.5}{f^{2}} \\ n (f) = 0.5 N (\frac{f l}{x_{p}}) \frac{1}{f^{2}} = 0.5 N \frac{l}{f x_{p}} \\ f = (x_{p} - x) / l \\ n (x) = 0.5 N \frac{l^{2}}{x_{p} | x - x_{p} |} \end{array}$

(1.11)

The number of atoms at distance |x_p-x| hitting the wall per second is then n(x)v_x|x-x_p|/v_x.

$n (x) \frac{v_{x}}{| x - x_{p} |} = 0.5 N \frac{l^{2} v_{x}}{{| x - x_{p} |}^{2} x_{p}}$

(1.12)

The mean free path is

$l = \frac{h x_{p}}{N a}$

(1.13)

where a is the radius of the hard disc atom.

Then equation (1.12) becomes:

$n (x) \frac{v_{x}}{| x_{p} - x |} = 0.5 N \frac{{(\frac{h x_{p}}{N a})}^{2} v_{x}}{{| x_{p} - x |}^{2} x_{p}} = 0.5 \frac{h^{2} x_{p} v_{x}}{N a^{2} {(x_{p} - x)}^{2}}$

(1.14)

Now we must integrate this expression over all the x's from 0 to x_p.

$\begin{array}{l} 0.5 \frac{h^{2} x_{p} v_{x}}{N a^{2}} \int_{0}^{x_{p} - l} \frac{d x}{{(x_{p} - x)}^{2}} = 0.5 \frac{h^{2} x_{p} v_{x}}{N a^{2}} [\frac{1}{x_{p} - (x_{p} - l)} - \frac{1}{x_{p}}] = \\ 0.5 \frac{h^{2} x_{p} v_{x}}{N a^{2}} (\frac{1}{l} - \frac{1}{x_{p}}) \approx 0.5 \frac{h^{2} x_{p} v_{x}}{N a^{2} l} = 0.5 \frac{h^{2} x_{p} v_{x} N a}{N a^{2} h x_{p}} = 0.5 \frac{h v_{x}}{a x_{p}} \end{array}$

(1.15)