Gas Compression through A Nozzle

Introduction

This animation shows the periodic compression and expansion of a gas by a moving piston. The original idea here was to show how a wind is generated by a gradient in atomic density. An extreme gradient is generated here by having a nozzle at the right side of the cylinder and having an almost perfect vacuum beyond the nozzle.

In order to show significant results, we will permit piston speeds that are approximately equal to the average thermal speeds of the atoms. This will show how interesting atomic density distributions can build up on the face of the advancing piston. What is interesting is that we can get reasonably good agreement for energy, force on piston, and average atomic speed between the hard sphere kinetic calculations and first principles results derived from classical gas pressure theory analysis. This agreement exists even though the gas is never in a quasi-static state.

Figures

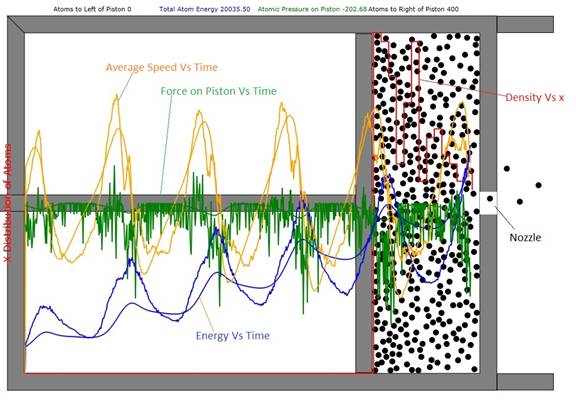
Figure 1: Cylinder and Piston filled with 400 atoms. The total atom energy has increased from about 3500 to 20036 units. By viewing the red histogram, one can see that the density of the atoms to the right of the right-going piston is highest. This is because piston speed slightly exceeds average atomic speed so the atoms can't diffuse away fast enough. The smooth blue curve is the first-principles result for the total atom energy and the smooth green curve is the first principles result for the force on the piston. The orange curves give the average velocity in the horizontal direction.

Calculation of Energy during adiabatic compression

Adiabatic compression means that no heat flows into the system under observation during that compression. Atoms do gain kinetic energy (the temperature increases) during adiabatic compression because of the mechanical energy provided by the moving piston. The reason is that a atom with x velocity component -v_x (where v_x>0 for the time being) that collides with the front side of a piston moving in the x direction at speed v_p>0 rebounds with an x component of speed v_x+v_p i.e.

and therefore the colliding atom gains energy.

We will use the term "front side" to describe the face of the piston whose outward normal is parallel with v_P and the term "back side" to describe the face of the piston whose outward normal is anti-parallel with v_P.

One might object that the opposite speed change happens when an atom hits the back side of the piston and that is absolutely correct. However, as the animation shows, there is often a much higher density atoms on the front side of the piston than the back side and therefore there is a net energy gain per cycle.

In the following, we will consider only the motion of the piston in the positive x direction. By symmetry, the results for energy transfer for motion in the negative x direction must be the same. Also we set the piston coordinate, x_P, to zero when the piston is at the center of the cylinder.

The average time between collisions of the atom with the front of the moving piston is

and the time between collisions with the back of the moving piston is

where L is the total length of the cylinder and <v_x> is the average x component of the velocity.

where E_total is the total kinetic energy of the atoms and N is the total number of atoms.

The total rate of collision on the front and back side is then just the number of atoms, N, on that side divided by its average interval between collisions:

The energy transfer per collision is just due to the added or reduced x component of velocity due to the moving piston:

where m is the mass of the atom and v_p can be positive or negative.

Then the rate of energy added per second to atoms colliding with the front of the piston is :

and the rate of energy subtracted per second from atoms colliding with the back of the piston is:

So the program continuously integrates the dE/dt increments to estimate the added kinetic energy associated with the periodic adiabatic compressions. Of course here, x_p and v_p vary sinusoidally with time.

Calculation of Force on Piston

The net force on the moving piston due to atoms hitting it is calculated in an entirely similar way to the energy induced in the atomic gas by the piston. First we have the rates of atoms hitting the front and back of the piston:

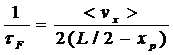
The momentum imparted to the moving piston for each collision averages:

And therefore the total momentum in the positive x direction imparted per second from all the atoms hitting the front and back of the piston is:

and therefore the total force on the piston is:

Obviously, if N_F=N_B we have a force on the piston even when v_p=0. That is reasonable, since, when, for example, x_P>0, the gas on the right side is compressed.

Calculation of Average Atomic Horizontal Speed

Again, we have the average rate of collisions with the moving piston:

and with each collision we expect the atom to gain speed v_p. Then the added speed in +x direction would be:

where both the numerator and denominator vary sinusoidally.