Fit of Binomial Distribution (Pascal’s Triangle) to a Gaussian

 

Introduction

            Many processes in the real world can rely on situations where there are only two possible outcomes.  A really important example of this is heredity of biological genes but quite a few genetic inheritance cases are more complex than simple binary.  So, here, we will consider the simple situation where N coins are tossed and can land with either heads or tails showing.

            It is useful and instructive to develop a simple algebraic model of the probabilities of the number of heads.  Although it is well known that the probabilities are given by the binomial distribution, this distribution becomes unwieldy when the number of coins tossed per throw is large because of the very large factorials involved.  Therefore I chose to fit these probabilities to a simple Gaussian curve since that is the basis of many statistical analyses.  The factorials in the binomial distribution can be well approximated using Stirling’s formula and that is what I have used below.   

Use of Stirling’s Approximate Formula for the Factorial

Stirling’s expression for the factorial of k is

                                                                                                                 (1)

and is accurate to within about 1/2% when k is 7 and much more accurate for larger k.  A very simple Taylor’s series expansion enhances the accuracy of equation 1 for k<7. 

http://en.wikipedia.org/wiki/Stirling's_approximation

Maximum Value of Probability

            Since our experiment involves the probability of only 2 different ways the objects can land, if N is the number of items thrown, then the total number of possible ways that the items can land is 2N.  Using the binomial theorem we have the maximum probability:

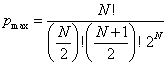                                                                                                  (2)

where, in the denominator, the N/2 and (N+1)/2 are integer values.

Using expression 1 in equation 2 we have:

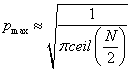                                                                                                           (3)

 

where

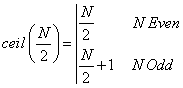                                                                                              (4)

For notation simplicity we will henceforth use the symbol Nc=ceil(N/2).

Width of Gaussian

            The width of the Gaussian involves taking the logarithms of the Stirling equivalent of equation 2.  The probability ratio at k=Nc+dN  to that at the peak value is:

                                                                                (5)

where I have set this ratio to 1/e.

 

Inverting equation 5 and using Stirling’s equation we obtain:

                                                                 (6)

Taking the logarithm of both sides of equation 6 we get:

                                  (7)

For fairly large Nc it is valid to make the approximation:

                                              

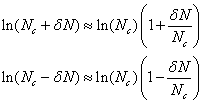
Then equation 7 becomes:

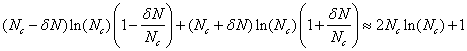   (8)

Collecting terms in equation 8 we have:

                                                                                                                           (9)

 

so that

                                                                                                                       (10)

Note that in equation 6 we have neglected the square root terms in equation 1.  If included, these will lead to an additional term -dN2/(2Nc2) on the left side of equation 9.  Since Nc>>1 this term will not appreciably change the result in equation 10. See Figure 1 below for the results.

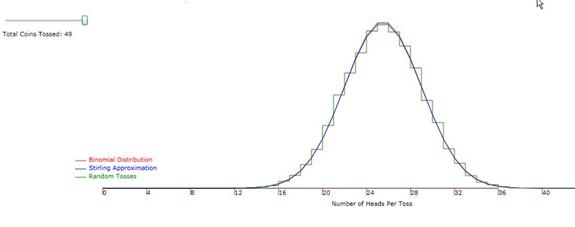
Figure 1: Fit of binomial distribution to a Gaussian with parameters computed from the Stirling Approximation for the factorials in the binomial distribution.  Also shown is the distribution (random tosses) obtained by using the computer’s random number generator.