Gravity Assist Animation
Introduction
Propellant for probes to other planets in our solar system
can be greatly reduced by use of close flybys of planets. The main reason for this is that the planet
has a lot of orbital speed so that, when the spacecraft is under its
gravitational force influence, the planet tends to make a component of the spacecraft's velocity equal to its own
orbital speed. This effect is explored
by this animation.
Figures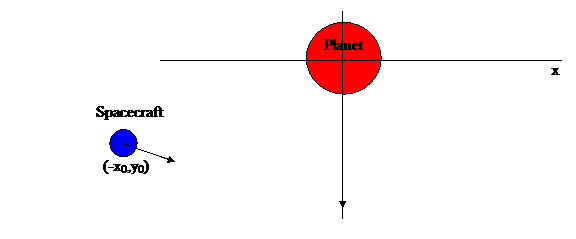
Figure 1:Diagram of the initial positions of the
spacecraft and the planet. In order to
provide energy to the spacecraft, the planet has more speed than the
spacecraft.

Figure 2: Diagram of the animation showing closest
approach of spacecraft to planet under influence of gravity attraction.
Math for Computing Starting Conditions for Close Intercept
We will assume the planet starts at y=0 and is moving
downward at speed vyp along the y axis.
The spacecraft, at the start, is poised farther down at -y0
and in the x direction at -x0 from the y axis where both x0
and y0 are positive numbers.
The initial velocity of the spacecraft will be (vx0,vy0). We need to be able to compute the appropriate
distance x0 from the y axis for the start position of the
spacecraft. Without any change in speed,
the time required for the spacecraft to cross the y axis is
|
|
|
(1.1)
|
For the spacecraft to intercept the planet which is on the y
axis we must then set a nominal value for x0 to be
|
|
|
(1.2)
|
The above values of the starting position for the spacecraft
would cause the intercept to occur at the center of planet.
We want to have the intercept occur with an offset, so,
from the rim of the planet. If the
radius of the planet is a, then the distance from the planet center is dint=a+so. A unit vector along the normal to the
relative velocity vector can be written in terms of the differential
velocities:
|
|
|
(1.3)
|
Then the normal ndv to the relative velocity
vector can be written:
|
|
|
(1.4)
|
To correct both x0 and y0 for the
offset and the radius of the planet we need to use this normal vector:
|
|
|
(1.5)
|
Effect of Gravity on Closest Approach
Obviously the slower the relative starting speed, the more
the effect of gravity on the final intercept distance. And the approach speed is constantly changing
due to gravity. At any center to center distance r, the acceleration, , due to
gravity is
|
|
|
(1.6)
|
where
|
|
|
(1.7)
|
Obviously the speed at any position will be affected by the acceleration:
|
|
|
(1.8)
|
and further the position will be influenced by this speed
change:
|
|
|
(1.9)
|
A more acceptable form of this equation has rp -rs
as the variable:
|
|
|
(1.10)
|
It is probably best to solve this equation for rs(t)
numerically and provide the results to the learner.
Energy Required for Course Correction After Gravity Assist
The spacecraft direction, arctangent(vy/vx), is changed by
gravity assist and it is important to consider how much energy is required to
correct the course. We can always make
this correction long after the gravity assist by applying force in the
direction normal to the present course.
The unit normal vector, nv,
to the spacecraft direction is given by:
|
|
|
(1.11)
|
We want to apply acceleration along this normal vector until
|
|
|
(1.12)
|
The power needed to cause this acceleration is
|
|
|
(1.13)
|
where F is the
force, m is the mass of the
spacecraft and a is the magnitude of
the acceleration. Using equation (1.11)
in equation 113 we have
|
|
|
(1.14)
|
So the power needed is identically zero as long at the
acceleration is normal to the current velocity.
That also means that the energy needed is identically zero. The reason for this strange result is that,
if a particle's velocity is zero, then it requires only infinitesimal energy
input to change the velocity by a small amount i.e. Ein=mvdv=0 when
v is zero. A physical analogy for this
behavior is that of a charged particle that has a magnetic field applied normal
to the plane of the particle's trajectory.
If the field is applied for a very short time, the path of the particle
will be an arc of constant radius. As is
well known, the particle will not change its kinetic energy due to the magnetic
field. The above result assumes that the spacecraft has left the influence of
the gravity on the planet.

