Statics of Two Masses Fastened to a Rigid Rod Under the Force of Gravity
Introduction
It is easy
to find simple horizontal statics tutorials on the
internet but I have not been able to find any that involve a tilted supports
with either two masses or non-uniform mass distribution. This animation should fill that niche.
Figure
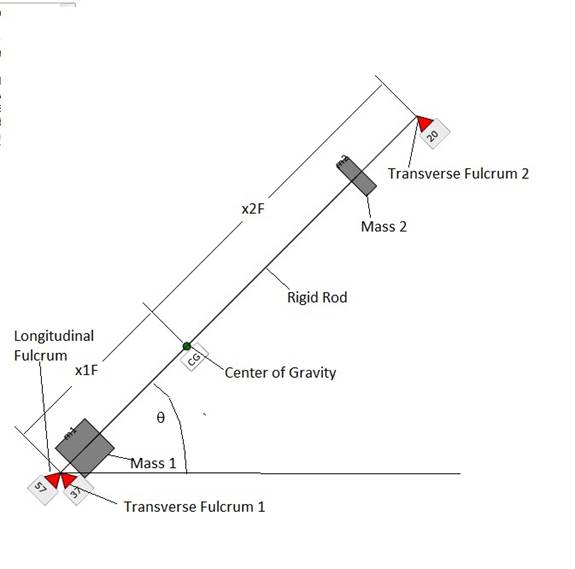
Figure 1: Showing the 3 fulcrums (scales) in red, the
rigid rod on which the masses are fastened, the masses, and the center of
gravity (CG) and distances from the fulcrums to the CG. Currently the longitudinal force is 57 when
the transverse forces are 37 and 20, respectively.
Calculations for Lumped Masses:
Let subscript t stand for transverse to the rigid rod and subscript l stand for longitudinal to the rigid rod. Since the rod is rigid, we may treat the problem as if there were only one mass M=(m1+m2), centered at the CG where xCG is
![]()

Note that the resultant of all 3 forces is Mg and points
upward. Also note that the upward
components of Ft are proportional to cos2(q), which for small q is extremely close to 1.
Calculations for Linearly Distributed Mass
For now, assume q=0 and let:
![]()
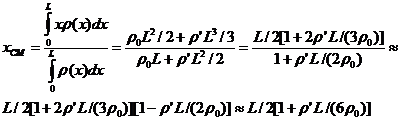
where the approximations apply for
small values of r'L/r0.
It's as if we had masses at x=0 and x=L of values:
![]()
where
![]()
and where the total mass is:
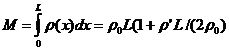
We can also model the system as having a single mass M at the CG and then use two fulcrums to balance the torques about the CG.
Now, letting q be
variable, we must balance the torques about the CG in order to avoid rotation. If r1
points from the CG to fulcrum 1 and r2
points from the CG to fulcrum 2 then the total torque about the CG is
zero when we have for the forces at transverse fulcrums 1 and 2:
![]()
where the carat above y indicates a unit vector. Note that
![]()
Resolving r1 and r2 into x and y components we have:
![]()
where the x's and y's with the 1 subscript have signs opposite to those with the 2 subscript. The values of x,y are:
![]()
Then the torque balance equation becomes:
![]()
Of course, when the centerline of the mass distribution is tilted at angle q, we must have a longitudinal restraining force
![]()
Just as before we have:
![]()
Note that the sum F1+F2 is
![]()
This is the force transverse to the line between the fulcrums. Its upward component is
![]()
The upward component of FL is
![]()
so that the sum of the upward
component of the forces at all 3 fulcrums is Mg, as expected.