Hall Effect Animation

Introduction

The Hall effect is due to a combination of two electromagnetic fields. The first, the electric field, E, results in an electric current in a resistor or a conductor. Then, if we have a magnetic field, B, directed perpendicular to the current, we will obtain another current that is perpendicular to both the original current and the magnetic field. This animation will show both currents as well as how they change when the E and/or the B fields are switched on or off.

The Hall effect is often used in three phase brushless motors to determine controller switching timing.

Figure

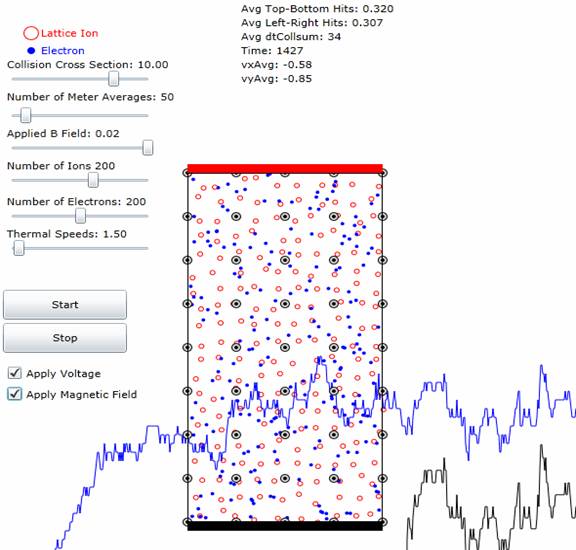
Figure 1: Picture showing the Hall Effect Screen. Applied voltage is indicated by the red and black bars at top and bottom. The magnetic field is shown as the circles with dots indicating vectors coming out the screen. The electrons drift upward and to the left due to the Hall effect.

Equations

The electric field, E, due to the applied voltage, V, is

$E = \frac{V}{h} \hat{y}$

(1.1)

where h is the height of the conductor/resistor. The current density, J, in the y direction is defined by:

$J_{y} = σ E$

(1.2)

where σ is the conductivity. Charges that are participating in this current density feel a force to the left equal to:

$F = q v \times B$

(1.3)

where q is their charge and v is their velocity, mostly in the y direction, and the x between v and B means the cross product. The form of equation (1.3) indicates that the cross product, vxB, is really another electric field, this time in the x direction. Therefore, using the same method as in equation (1.2) we can write the current density in the x direction:

$J_{x} = σ (v \times B)$

(1.4)

Now we should quantify the speed, v_y, of the charges in the y direction. We can do this by re-writing J_y in terms of this speed:

$J_{y} = n q v_{y}$

(1.5)

where n is the density of electrons.

Solving equation (1.5) for v_y we have:

$v_{y} = \frac{J_{y}}{n q}$

(1.6)

and substituting the result into equation (1.4) we have:

$J_{x} = \frac{σ J_{y} B_{z}}{n q}$

(1.7)