Thermal Engine Cycle Using Ideal Gas

Introduction

The usual gas thermal engine cycle involves two isothermal excursions along with two adiabatic excursions the last of which returns the working gas to its original pressure and volume as depicted on a plot of pressure versus volume. In this animation I have chosen to plot internal energy and volume separately versus time. At the same time I show the motion of the gas particles and piston while plotting these parameters. I think this removes some of the mystery of how isothermal and adiabatic excursions are achieved.

Figures:

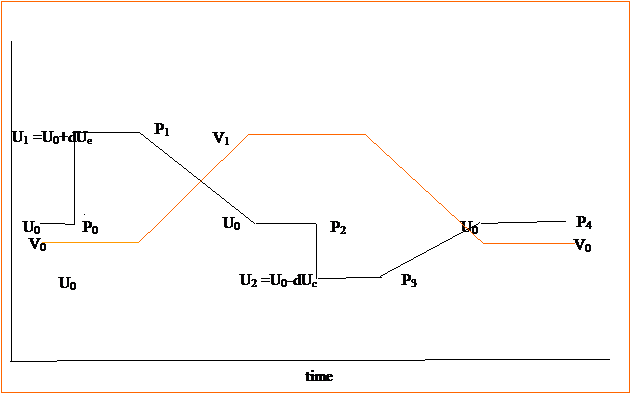
Figure 1: Internal energy, U and Volume, V as a function of time over a complete cycle. The cycle design adds heat at stage, then expansion at stage 2 back to the original internal energy U₀ . Then the internal energy is reduced by putting the gas in contact with a cooler region. Finally the gas is compressed back to its original internal energy, volume, and pressure to complete the cycle. Pressure is labeled P₀, P₁, P₂, P₃ and P₄ at the various stages of the cycle. Subscript e stands for expansion and c stands for contraction.

Figure 2:Animation experiment showing container and piston and gas particles along with plots of internal energy, U (black), pressure, P (blue), integral of Pdh (red) where h is piston height, calculated internal energy (green), UT, and piston height (orange).

Calculation of Energy per Cycle

The ideal gas law is:

$P V = c U$

(1.1)

where c is a constant that depends on the ratio of heat capacity at constant pressure to that at constant volume. For simple hard spheres and a 2 dimensional gas like we are considering here c=1 while for a 3 dimensional gas c=2/3. The actual value of c will not be important in the following calculations since these use only ratios of the quantities of interest.

From equation (1.1) we can write the pressures, P, at the various stages of the cycle as:

$\begin{array}{l} P_{1} = P_{0} \frac{U_{1}}{U_{0}} \\ P_{2} = P_{0} \frac{U_{1}}{U_{0}} \frac{V_{0}}{V_{1}} \\ P_{3} = P_{0} \frac{U_{1}}{U_{0}} \frac{V_{0}}{V_{1}} \frac{U_{2}}{U_{0}} \\ P_{4} = P_{0} \frac{U_{1}}{U_{0}} \frac{V_{0}}{V_{1}} \frac{U_{2}}{U_{0}} \frac{V_{1}}{V_{0}} = P_{0} \frac{U_{1} U_{2}}{U_{0}^{2}} \end{array}$

(1.2)

However, since in stage 4, both the volume and the internal energy are the same as in stage 0, we must conclude:

$\begin{array}{l} P_{4} = P_{0} \\ \frac{U_{1} U_{2}}{U_{0}^{2}} = 1 \end{array}$

(1.3)

$\frac{(U_{0} + d U_{e}) (U_{0} - d U_{c})}{U_{0}^{2}} = 1$

(1.4)

We can solve for dU_c in terms of U₀ and dU_e

$\begin{array}{l} (U_{0} + d U_{e}) (U_{0} - d U_{c}) = U_{0}^{2} \\ (d U_{e} - d U_{c}) U_{0} = d U_{e} d U_{c} \\ d U_{c} (U_{0} + d U_{e}) = U_{0} d U_{e} \\ d U_{c} = \frac{U_{0} d U_{e}}{U_{0} + d U_{e}} \end{array}$

(1.5)

Since dU_e is greater than dU_c we deduce, from conservation of energy, that we can obtain macroscopic work

$d W = d U_{e} - d U_{c}$

(1.6)

from the piston. The amount of work can be obtained by solving line 2 of equation (1.5) for dU_e-dU_c

$d U_{e} - d U_{c} = \frac{d U_{e} d U_{c}}{U_{0}}$

(1.7)

The efficiency, η, of the cycle is the work obtained divided by the amount of heat input during the first part of the cycle:

$η = \frac{d U_{e} - d U_{c}}{d U_{e}} = \frac{d U_{c}}{U_{0}} = \frac{d U_{e}}{U_{0} + d U_{e}}$

(1.8)

Since U is always proportional to temperature we can rewrite equation (1.8) as:

$η = \frac{T_{H} - T_{0}}{T_{H}}$

(1.9)

Where T_H is the highest temperature and T₀ is the base temperature. Equation (1.9) is recognizable as the expected relation between efficiency and temperatures. Note, however, that this treatment never brought up the mystical concept of entropy.

Calculation of Internal Energy during Expansion or Contraction

Both the internal energy and the pressure are changing during volume change. Using equation (1.1) we can write

$U = \frac{P V}{c}$

(1.10)

$U (V) = U_{1} \frac{V_{0}}{V}$

(1.11)

where V₀ is the starting volume and V is the volume at any part of the volume change phase. The red plot shows that the internal energy change is proportional to

$U (V) - U (V_{0}) = \int_{V_{0}}^{V} P d V$

(1.12)