Speed On Hills with no Driving force

Introduction

This is the derivation of equations for speed versus position and time where there is neither outside force or environmental drag force

Equations:

1. Sufficient Speed and Initial Elevation to Ascend Hills:

Conservation of momentum requires that:

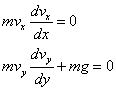(1)

These two equations can be combined and integrated to yield:

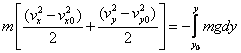(2)

where this equation states conservation of energy.

The hill profile is provided by the dependence of y on x is:

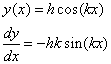(3)

Therefore the energy equation becomes:

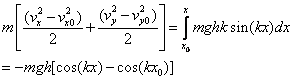(3)

where x₀ is the starting x coordinate.

Solving for v_x²+ v_y² we have:

(4)

And we know that:

(5)

Then equation 4 becomes:

(6)

Let

(7)

Then we can solve for v_x and obtain:

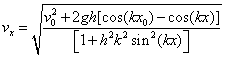(8)

To obtain a result for t(x) we need to solve the integral where dx/v(x)=dt are the integrands:

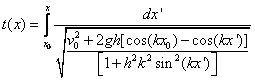(9)

For the case where v₀²>0 the integral can be quite accurately converted to a sum:

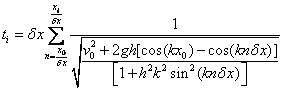(10)

where dx<<1/k.

We’d also like to know the dependence of x and y on t. If we save the data from equation 10 in 2 arrays, t_i and x_i, then ith element of x corresponds to the ith value of t.

2. Insufficient Speed and Initial Elevation to Ascend Hills

This section treats the case where:

for at least some values of x. Since the particle starts with non-zero speed at x₀, the maximum y that can be attained is:

(11)

This value of y_max corresponds to the range of x:

(12)

Obviously v becomes imaginary for x outside the range

The only possibility is that the mass must go backward down the hill when it reaches x₁ so that the x increments, dx, become negative.

Again using the conservation of energy, we have for the speed at any y(x)

(13)

Then, similar to before, we have the result for v_x(x):

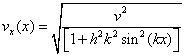(14)

The time, during the first trip from x₀ to x₁ for a given x would be given by an equation similar to equation 10:

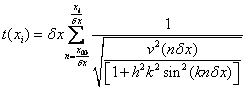(15)

However v²(x)-->0 at x=x₀₀ and x=x_1. To overcome this singularity, we must revert to another form for the y component of equation 1:

(16)

which can be solved for y:

(17)

However this solution is good only for kx<p. The solution for the entire range x₀ à x₁ is

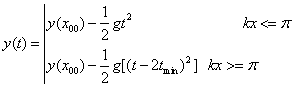(18)

where

(19)

Note that, by symmetry, the total crossing time is just 2t_min.

Also note that, when t=2t_min, y(t)=y(x₀₀)= y(x₁), as expected.

We may solve the above equations for t(x):

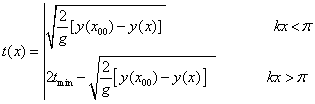(20)

The x coordinate Vs time on the first left to right trip is obtained by inverting the equation for y(x)

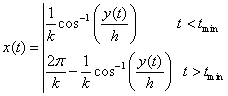(21)

To obtain the correct time dependence for subsequent trips back and forth, we use the following prescription:

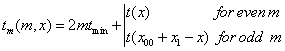(22)

where odd m corresponds to trips from x₁ to x₀ and even m corresponds to trips from x₀ to x₁. Obviously, t is a multi-valued function of x.