Speed On Hills with no Driving force
Introduction
This is the
derivation of equations for speed versus position and time where there is neither outside force or environmental drag force
Equations:
1. Sufficient Speed and Initial Elevation to Ascend Hills:
Conservation of momentum requires that:
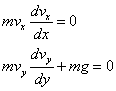 (1)
(1)
These two equations can be combined and integrated to yield:
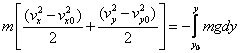 (2)
(2)
where this equation states conservation of energy.
The hill profile is provided by the dependence of y on x is:
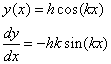 (3)
(3)
Therefore the energy equation becomes:
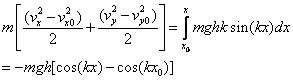 (3)
(3)
where x0 is the
starting x coordinate.
Solving for vx2+ vy2
we have:
![]() (4)
(4)
And we know that:
![]() (5)
(5)
Then equation 4 becomes:
![]() (6)
(6)
Let
![]() (7)
(7)
Then we can solve for vx and obtain:
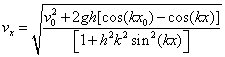 (8)
(8)
To obtain a result for t(x) we need to solve the integral
where dx/v(x)=dt are the integrands:
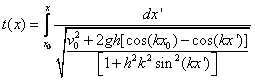 (9)
(9)
For the case where v02>0 the integral can be quite accurately converted to a sum:
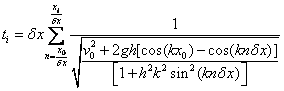 (10)
(10)
where dx<<1/k.
We’d also
like to know the dependence of x and y on t.
If we save the data from equation 10 in 2 arrays, ti
and xi, then ith element of x corresponds
to the ith value of t.
2. Insufficient Speed and Initial Elevation to Ascend Hills
This section treats the case where:
![]()
for at least some values of x. Since the particle starts with non-zero speed at x0, the maximum y that can be attained is:
![]() (11)
(11)
This value of ymax corresponds to the range of x:
![]() (12)
(12)
Obviously v becomes imaginary for x outside the range
The only possibility is that the mass must go backward down the hill when it reaches x1 so that the x increments, dx, become negative.
Again using the conservation of energy, we have for the speed at any y(x)
![]() (13)
(13)
Then, similar to before, we have the result for vx(x):
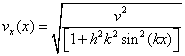 (14)
(14)
The time, during the first trip from x0 to x1 for a given x would be given by an equation similar to equation 10:
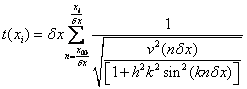 (15)
(15)
However v2(x)-->0 at x=x00 and x=x1. To overcome this singularity, we must revert to another form for the y component of equation 1:
![]() (16)
(16)
which can be solved for y:
![]() (17)
(17)
However this solution is good only for kx<p. The solution for the entire range x0 à x1 is
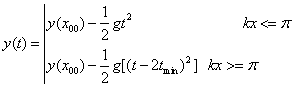 (18)
(18)
where
![]() (19)
(19)
Note that, by symmetry, the total crossing time is just 2tmin.
Also note that, when t=2tmin, y(t)=y(x00)= y(x1), as expected.
We may solve the above equations for t(x):
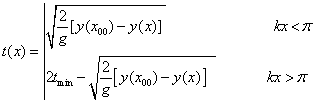 (20)
(20)
The x coordinate Vs time on the first left to right trip is obtained by inverting the equation for y(x)
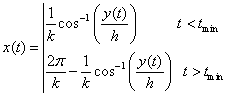 (21)
(21)
To obtain the correct time dependence for subsequent trips back and forth, we use the following prescription:
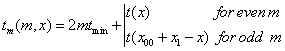 (22)
(22)
where odd m corresponds to trips from x1 to x0 and even m corresponds to trips from x0 to x1. Obviously, t is a multi-valued function of x.