LCR Oscillator Animation
Introduction
The LCR oscillator (LCR) is an exact analog of the harmonic oscillator shown under the Mechanics chapter. Its behavior goes a long way toward understanding the electrodynamics of the real world.
Calculations:
Switch Inductor L B field lines |Current| direction Resistor R Capacitor C![]()
![]()
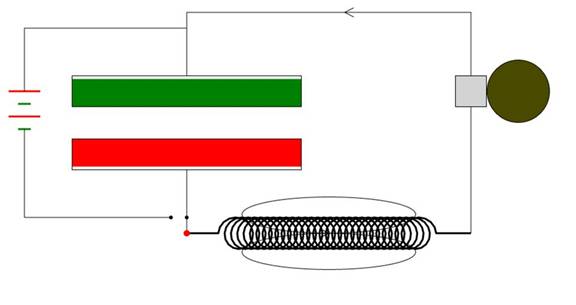
Figure 1: Circuit diagram showing the charging battery,
C, R, and L. Also shown is the charging
switch and the direction of the current that fills or depletes C. R is a light bulb which changes brightness as
current flows through it.
The picture above shows the
important parameters of the LCR. They include a capacitor, C, a drag element
(shown here as
Spring Constant=k
a light bulb with a resistance R ohms) and a
Inductance, L, which has an inductance of 1 Henry, at the bottom. The function of the capacitor is to trade off
energy between itself and the magnetic field of the inductance and the function
of the light bulb is to realistically simulate the decay of any oscillation
that is in progress.
The equation that describes the charge of the capacitor is:
![]() (1)
(1)
To solve equation 1 we make the substitution:
![]() (2)
(2)
where i is the square root of -1, Real[] denotes the real part of the resulting value, Q is the peak capacitor charge under any preset conditions, t is time, and wc (which has units of 1/time and is complex) is a parameter for which we will solve.
Using equation 2 in equation 1 we have very easily:
![]() (3)
(3)
The result for wc is:
![]() (4)
(4)
We see from equation 4, that if R=0 i.e. no resistive losses, then
![]() (5)
(5)
where we have defined w0. Also, to simplify notation, we now separate the real and imaginary parts of equation 4 by re-naming these quantities:
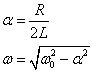 (6)
(6)
where a is the charge decay coefficient.
Using equations 6 in equation 2 we have
![]() (7)
(7)
Dielectric Slab Animation

![]()
Shown above is the dielectric slab in the capacitor gap. The rotation angle of dipoles, which are shown
as dumbbells with a red end and a green end, is animated. When the imposed
electric field is large, they are aligned anti-parallel to the electric field. This is the effect of a dielectric slab in a
capacitor: Since the slab’s dipoles align opposite to the imposed electric
field they cancel a large fraction of that field and therefore a larger charge
on the red and green plates is required to achieve the came voltage across the
capacitor. When the imposed electric
field is small or zero, the orientation of the dipoles becomes random as can be
seen from the animation
Summary
The meaning of equation 7 is that, if we initially charge
the capacitor to value Q, then the subsequent charge will follow the product of
the cosine periodic behavior times the exponential decay coefficient.