Linear quadrupole mass analyzer
Introduction
Linear electric quadrupoles (LEQ) driven at radio frequencies (rf) are used to detect the charge to mass ratios, q/M, of ions. When ions are injected along the axis of the LEQ, there is a sharp cutoff of the rf frequencies at which a given q/M ratio ion remains stable. Other q/M ratio ions have diverging amplitudes in the quadrupole and are not collected along the axis by the detector (usually an electron multiplier).
Most LEQ are configured as four long parallel conductive cylinders arranged in the form of a cruciform (see cross-section in Figure 1). At any one time a positive potential is applied to one opposite pair (say the horizontal pair) and a negative potential is applied to the other pair. This causes the potential between the positive potential pair to have an almost perfect parabolic potential distribution (see Figure 2) with minimum at the center (so that a positively charged ion will be restored to the center) while the negative potential pair will have a parabolic potential distribution with a maximum at the center. Thus the LEQ forms a “parabolic” potential well and the dynamics of particles will be the same as those of a harmonic oscillator. My original intent was to find a way to devise a true 2 dimensional parabolic potential well where the harmonic oscillator quantum states would be confined but that intent is not realized by the LEQ.
The equation which defines the potential in the cross-section of the LEQ is
![]()
where V0 is the voltage on the horizontal pair, r0 is the distance from the axis of the LEQ to the nearest edge of any of the cylinders, x is the horizontal displacement from the axis, and y is the vertical displacement from the axis.
Once the
initial displacement (x,y)
and the initial velocities (vx, vy)
of the charged particle is provided (via the sliders in the program), the
subsequent displacements are computed using Runge-Kutta
4th order integration. This
integration converges only for “Natural” frequencies less than about 10 Hz.

Figure 1: Contour plot
of the electric potential in the cross section of an LEQ. Note that the potential forms a saddle at the
center of the LEQ with maxima along the horizontal axis and minima along the
vertical axis for the potential shown on the poles. Of course, the maxima and minima axes will be
reversed when the voltages on the poles are reversed.
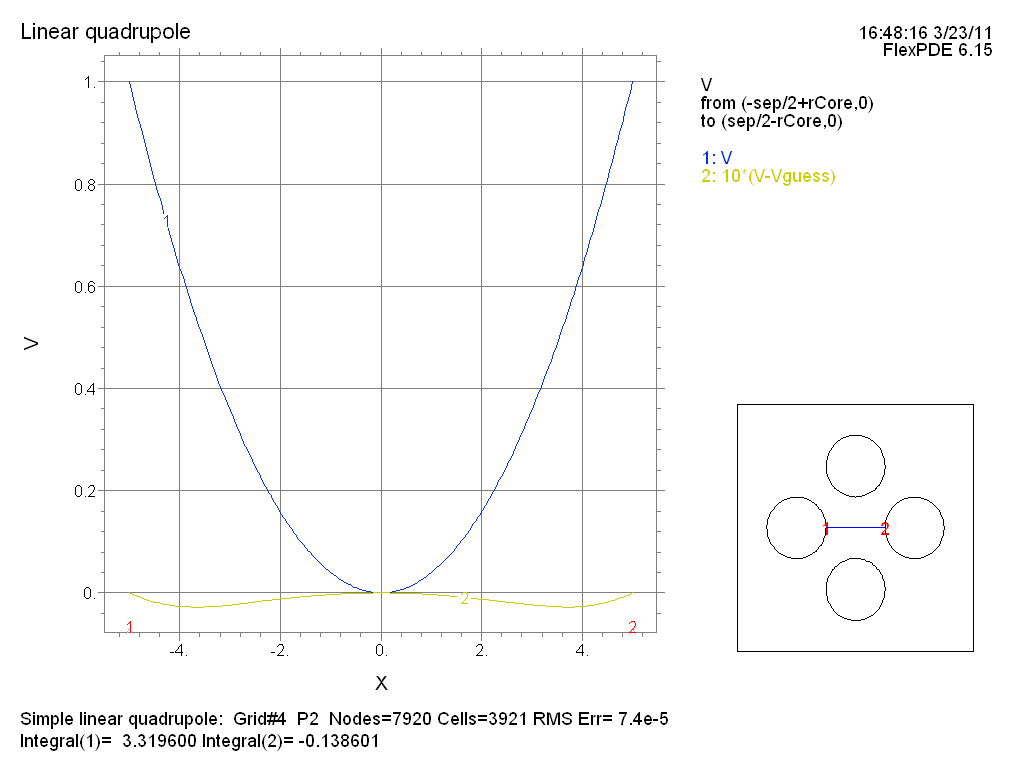
Figure 2. Demonstration that the potential between the horizontal poles (see blue line in inset) is a parabolic potential well. The yellow line is a plot of the 10 times the difference between the actual potential and a perfect parabola.