Laser Parameters
Introduction
A laser is a type of oscillator. Oscillators are characterized by several properties:
1. They have access to external power that gives them gain.
2. The gain exhibits a certain amount of spontaneous power emission prior to providing stimulated emission. Gain is initially greater than optical loss but always becomes equal to optical loss in steady state operation.
3. Feedback is provided by reflections from the local environment (such as mirrors).
For lasers, the external power is generally used to raise the atomic excitation of the gain atoms to a higher level than the ground state. As we will discuss later, if the laser radiation is to be continuous wave (CW) then the higher level cannot be the one just above the ground state.
The natural power emission of the gain medium is just that discussed in the “Quantum” chapter under Black Body Radiation (BBR). It is dependent on temperature and wavelength (or optical frequency) via Planck’s BBR equation.
For a standard linear laser, the round trip optical loss (including useful power output) of the feedback mechanism has to be less than the optical gain per round trip in the laser.
Figures:
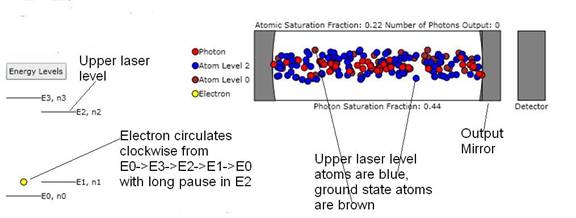
Figure 1: Shows both the Energy Level Diagram and the Confocal Resonator with photons, gain atoms, and ground
state atoms.
Pumping Rate Required to Achieve Lasing Threshold
For a simple atomic laser, the laser wave must compete with two processes in order to become a good collimated beam.
- Spontaneous Emission (SE): SE is invoked by the residual vacuum state of the bosonic photon gas which has one photon per directional mode. It occurs in all directions while the laser beam usually encompasses only one or a few directional modes. The rate of spontaneous emission depends slightly on temperature but that dependence will be ignored here.
- Optical losses: Since the round trip feedback is never quite 100%, the laser gain associated with the atomic inversion must be more than enough to overcome the optical losses.
Gain
The optical gain per laser round trip is described by the equation:
![]()
where n (m-3) is the density of inverted atoms, s (m2) is the cross section for stimulated emission, and Lg (m) is the length of the gain region traversed in a round trip of the resonator. The gain per unit length is:
![]()
Spontaneous and Stimulated Emission
The number of electromagnetic modes in a given frequency interval, Df, is
![]()
while the (usually small) number of
modes that are above threshold in the laser will be called pL.
Then if the average transit time from the upper laser level 2 to the lower laser level 1 is t21 the spontaneous emission the rate of spontaneous emission from atoms in level 2 is:
![]()
The Einstein relation between the stimulated coefficient (B) and spontaneous coefficient (A) is:
![]()
But we can state that B21 is equal to the following expression:
![]()
where g(f) is the line shape function and integrates to 1 over all frequencies
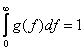
so that, for a simple rectangular line shape centered at f0, we would have
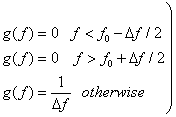
Then we can combine the above equations to get an explicit expression for A21:
![]()
The probability of stimulated emission is expressed as
![]() (B2)
(B2)
![]() (B3)
(B3)
where u(f) is the energy density per Hz, and f is the photon density.
![]() (B4)
(B4)
Atomic Energy Level Differential Equations
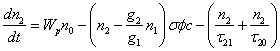 (B5)
(B5)
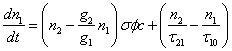 (B6)
(B6)
![]()
Let n1=0 and t10=0 and N=n0. Then from equations B5 and B6 we have
![]() (B7)
(B7)
where the fluorescence decay time from the upper laser level (2) is:
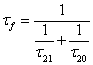 (B8)
(B8)
The pumping rate is expressed as
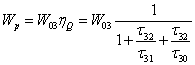 (B9)
(B9)
where hQ is the quantum efficiency for pumping from the ground state to the pump band (3).
Setting dn2/dt=0, we can solve equation B7 for the steady state f in terms of Wp, n2, and n0:
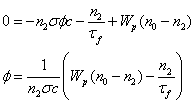 (B10)
(B10)
Further:
![]() (B11)
(B11)
and gain per round trip is:
![]() (B12)
(B12)
where l is the round trip loss. Then we have:
![]() (B13)
(B13)
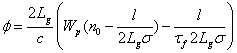 (B14)
(B14)
The vacant resonator decay time, tr, is expressed in terms of the round trip loss as:
![]() (B15)
(B15)
where 2L is the round trip optical length of the resonator so that equation B14 can be re-expressed as:
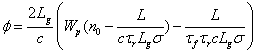 (B16)
(B16)
For a good 4-level laser material and a reasonably high output transmittance, the resonator decay time, tr, is much shorter than tf.