Energy Equilibration between a Lattice and Electrons

Introduction

We have already seen an animation of energy equilibration between two gases of different mass and different average initial energy. In the present animation we will see how energy is equilibrated between thermal energy of relatively free electrons and a lattice which is made up of massive nuclei (we'll call that particle an ion for brevity) that are harmonically bound to periodic lattice points and have zero initial energy.

Figures

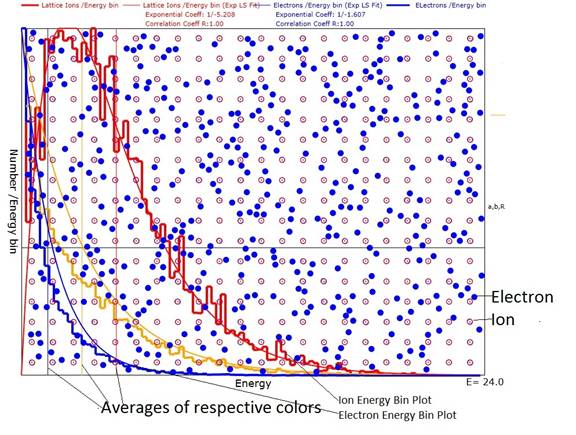
Figure 1: Showing the electrons as blue randomly distributed and the ions as red situated at lattice points. Also shows the histograms as well as the least squares fits of the electron and ion and sum distribution.

Calculations

Note: In the following, we will use lower case symbols for the free mass's parameters and upper case symbols for the bound mass's parameters.

1. One dimensional calculations:

As a warm-up, we will first compute the conservation of momentum and energy for a one dimensional free electron and anchored nucleus. The equation for momentum are:

Since the total momentum after the collision is the same as that before the collision, we can simplify the calculations by letting dp represent the change of momentum for each mass.

and those for energy are

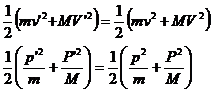
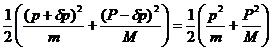
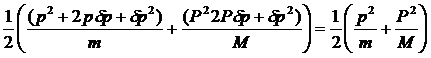
The displacement of M with respect to its rigid anchor point is expressed by

where A is the amplitude just prior to collision.

The momentum of M is also expressed as a function of time in the following manner:

Immediately following the collision, the displacement of M has not changed but the momentum and energy have changed. We can write:

(0)

where A and dq are presently unknown. The new amplitude A' can be found from the energy conservation equation:

where k is the constant of the linear restoring force, F(x):

To obtain dq, we use the fact that, immediately after the collision the displacement must be the same as just before the collision:

(1)

Getting both the sin and cosine terms in wt+q₀+dq we can have a fail-safe equation for dq:

Using equation 1 to express A' in terms of A we have:

Let's look at the difference P'²-P² at the time of the collision:

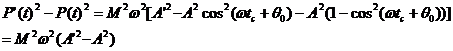
which should have been expected.

This is another expression of the energy change due to collision. Notice that the difference is independent of the time of the collision. Let's set this equal to the kinematic energy difference:

which gives us another expression for A'. This completes the analysis for 1 dimension.

2. Three dimensional calculations:

Here we will consider spherical particles which have the different masses, m and M, and diameters, D₁ and D₂. The centers of the free/anchored spheres will be labeled (x,y,z) and (X,Y,Z). Upon collision, the momentum transferred between the spheres will always be along the unit vector between their centers:

(2)

where

is the distance between centers. Since the animation is illustrated in only 2 dimensions, the collision analysis will assume a containing box that is large in the x and y dimensions but very thin in the z dimension. The following vector mathematics is correct for either 2 or three dimensions.

The expression for the final momenta in terms of the initial momenta is:

(3)

where the apostrophe on the left side of the equations indicates the final velocities. We know that the energies are conserved so

(4)

The directions of the change in momenta are along the vector of centers, u, and the values of the changes of momenta must be equal and opposite.

(5)

where m has units of mass and is still to be determined. Using equation 5 in equation 3:

(6)

Now we can use equation 6 in equation 4 to solve for the value of Mdv.

(7)

where the large dot stands for the dot product and equation 7 simplifies to:

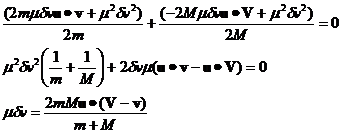(8)

We can now make the identification:

(9)

where m_r=m/2 is known as the "reduced mass".

Equations 6 and 8 are a complete solution for the final momenta. The final velocities are computed by dividing both sides of equations 6 by their respective masses:

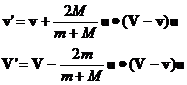(10)

Viewed as a harmonic oscillator, we have the following equations for displacement of M at the time of the collision:

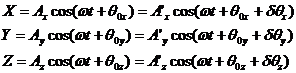(11)

where the result on the right is for just after the collision. For convenience I will assume that the restoring force is the same in all three directions so there is only one w. Since A_x and q₀ are known, Equations 11 can be solved for either A' or dq.

The velocity components in all three directions can be written from equation 11:

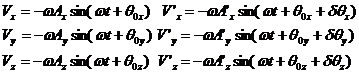
Just as for the one dimensional case, we will equate the energy changes in the harmonic oscillator case with the energy changes in the hard sphere collision case as given below:

Similarly we can write the components of V'-V in terms of the harmonic oscillator velocity components:

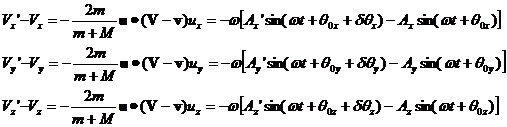(12)

Equations 12 can be solved for either A' or dq, which ever has not been obtained from solution of equations 11.

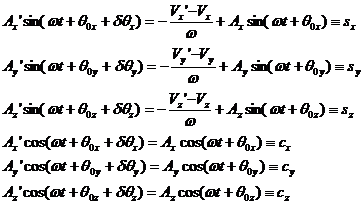(12)

Using the definitions s_i and c_i and the atan2(y,x) function, we have fail-safe solutions for dq:

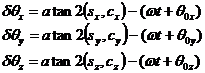
Similarly we obtain the solutions for A':

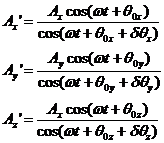
Summary

The result of the animation is that the energy per particle obtained by the ions is greater than that obtained by the electrons. A reasonable fit to the ion energy density distribution is:

where a_I and b_I are parameters found by a 2-dimensional Newton-Raphson technique that minimizes the residual errors between N_I(E) and the ions per energy bin found by iteration of collisions. Similarly the electron energy density must be fit by a distribution like the following:

It is presently believe that the reason that the ions end up with more energy per particle is that they can store any energy that they obtain in their restoring potentials.