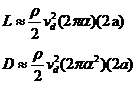Atomic Model of Airfoil Lift and Drag
Introduction
In PhysicsAnimations.org under the chapter "Gas Physics", I've already shown that all of the statistical laws of gas physics can be obtained from numerical atomic models if atom-atom collisions are taken into account. In the present animation, I am showing that the standard laws of Airfoil lift and drag can also be reasonably obtained from numerical atomic models. What is new is that I show that a standard assumption, that the gas can be assumed to be incompressible, is not justified even for free stream flow rates that are much lower than Mach 1. In fact, the argument that the lift is due to the differences in density (compression) between the bottom of the airfoil and the top, seems to be justified for a particle approach like the present one.
Figures
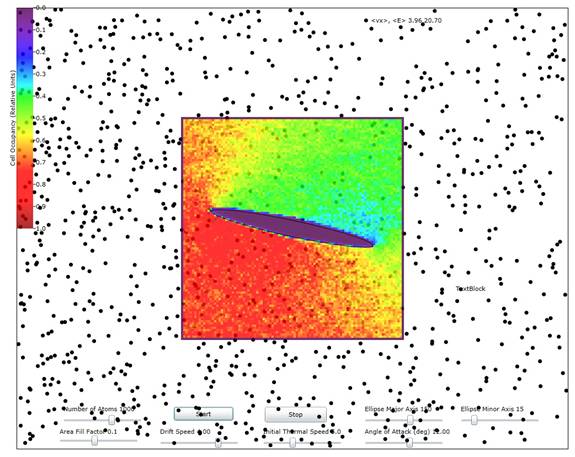
Figure 1: Showing the cell occupancy (average density) when the drift speed is about 60% of the mean thermal speed and with a 12 degree angle of attack. The relative scale for the density is shown in the color stripe at the left.
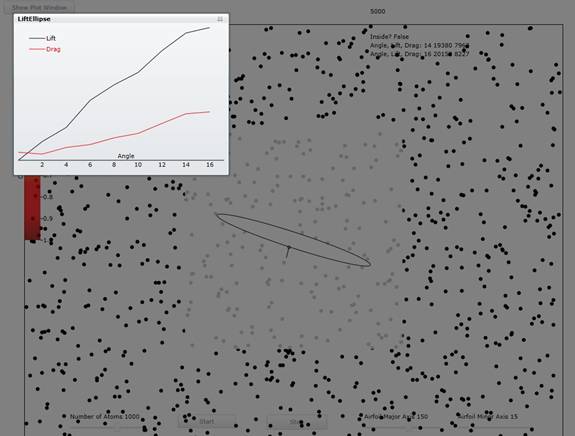
Figure 2: Showing the lift and drag Vs angle when the drift speed is 60% of the
average thermal speed from 0 to 16
degree angle of attack. Note the
characteristic linear relation for the lift and quadratic relation for the
drag.
Physics and Math of Particle Approach
In other topics under the chapter "Gas Physics" I've documented the physics of particle-wall collisions and of particle-particle collisions. So here I will confine my remarks to atom collisions with the airfoil. Here I've chosen an airfoil shape that derives from complex numbers called Joukowski airfoil.
Since the atoms are flowing (drift speed) rather than the airfoil moving, the wing does not give up energy to the atoms and that means that their collisions with the wing conserve energy. To conserve energy, the two orthogonal components of the exiting atom's velocity must have the sum of their squares equal to the sum of the squares of the incident velocity components. For a smooth surface, the usual assumption is that the exiting velocity component tangential to the airfoil surface is the same as the incident tangential velocity component. That means that the exiting velocity normal to the airfoil has to be opposite to the incident velocity component. On a very fine spatial scale, no surface is smooth with respect to the de Broglie wavelength of the atoms (approximately 0.05 nanometers for air at room temperature). However, the assumption above will represent a reasonable average for the behavior of the atoms that hit the airfoil.
Joukowski Airfoil
Let Z be the coordinates of the original circle in the complex plane. Let the radius of this circle be
![]()
where a and b are the horizontal and vertical semi-axes of an ellipse to which this airfoil will reduce with no x and y offsets for the original circle.
Also define the parameter
![]()
Let the x and y offset of the center of this circle from z=0 be
![]()
Then the airfoil boundary is formed by the expression:
![]()
where Z is described parametrically by:
![]()
Finding the normal vectors of the airfoil boundary
We define an array of points, zB, Vs angle q along the boundary of the airfoil. Then the tangent vector at each of these points is given by the complex vector:
![]()
and the outward normal vector is obtained from the tangent vector by the simple expression
![]()
Determine if a point (or particle) is inside or outside the Joukowski airfoil
In order to know when a particle collides with the boundary, we need to distinguish whether any part of the particle is inside the boundary.
When defining the airfoil boundaries in the previous section, we need to save two arrays. First save an array, zB, of the points of the boundary. Then use this array to compute an array, n, of the outward normal vectors of the boundary at all the boundary points. To determine if a point, z, is inside the boundary compute all the magnitudes
![]()
and find index, ic, of the least magnitude. This ic will be the closest boundary point to the point z. Now form a vector that points from the zB[ic] to z. Then take its dot product with n[ic]. If the dot product is negative, then the point is inside the boundary. Otherwise it is outside. This method is simple and fast for all boundaries that are not re-entrant, i.e. for all boundaries that don't form more than one loop. The problem with more than one loop lies in the fact that the method for computing the outward normal becomes more complicated for this case. One would have to build re-entrant recognition into the normal calculating algorithm.
Using the Normal Vector to Compute the Lift and Drag
Contributions at Each Impact
First we compute the dot product of the momentum vector with nxy.
![]()
Then we compute the change in the momentum vector
![]()
The y component of this is the contribution to the lift, L
![]()
and the -x component of it is the contribution to the drag D:
![]()
Comparison of Animation Results with Standard Equations
For 2 dimensional space, the standard equations for lift and
drag of a thin symmetrical airfoil at low angle of attack are (see
http://www.grc.nasa.gov/
where vd is the drift speed of the air along the x direction and r is the air mass per unit area. The result of equation for the simulation, at, say 10 degrees or 0.16 radians, with 2a=300, vd=2.5, r=0.00125 is L=1.29. The animation result for the same conditions is L=1.65. Therefore, the lift results for the animation are reasonably in agreement with the standard thin airfoil expressions.
Conclusions
Although the animation results in lift and drag numbers that are comparable to real world values, it is clear that some real world experiments that obtain difference in the speed of air flow over the top and bottom of the airfoil disagree with those obtained in the animation. Thus there must be a more complex interaction at the boundary layer at the surface of the airfoil. Since there are many real world cases where air viscosity can be neglected, we are left only with the (sub)microscopic roughness of the airfoil to explain how the airfoil re-shapes the contours of constant air velocity on its top and bottom.