Atomic Model of Airfoil Lift and Drag

Introduction

            In PhysicsAnimations.org under the chapter "Gas Physics",  I've already shown that all of the statistical laws of gas physics can be obtained from numerical atomic models if atom-atom collisions are taken into account.  In the present animation, I am showing that the standard laws of Airfoil lift and drag can also be reasonably obtained from numerical atomic models.  What is new is that I show that a standard assumption, that the gas can be assumed to be incompressible, is not justified even for free stream flow rates that are much lower than Mach 1.  In fact, the argument that the lift is due to the differences in density (compression) between the bottom of the airfoil and the top, seems to be justified for a particle approach like the present one.

Figures

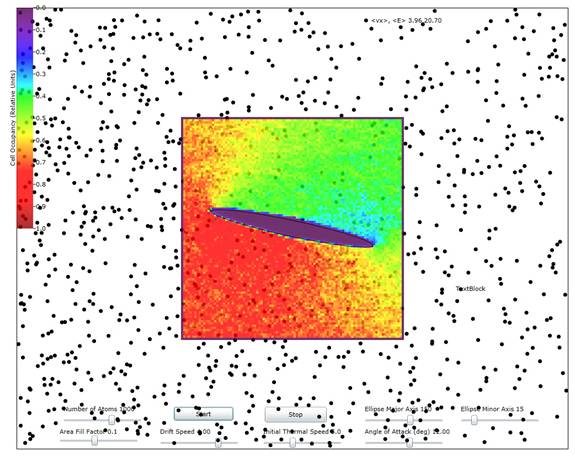
Figure 1: Showing the cell occupancy (average density) when the drift speed is about  60% of the mean thermal speed and with a 12 degree angle of attack.  The relative scale for the density is shown in the color stripe at the left.

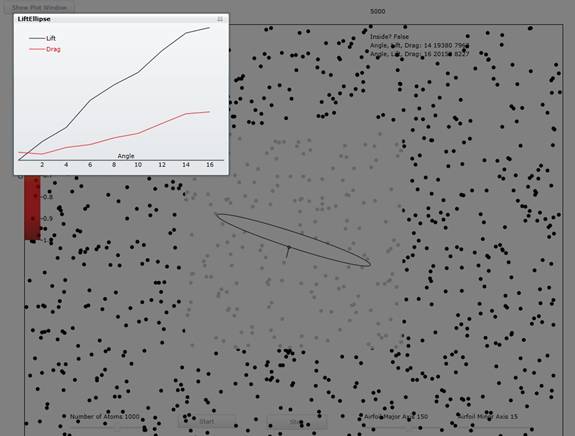
Figure 2: Showing the lift and drag Vs angle  when the drift speed is 60% of the average  thermal speed from 0 to 16 degree angle of attack.  Note the characteristic linear relation for the lift and quadratic relation for the drag.

Physics and Math of Particle Approach

            In other topics under the chapter "Gas Physics" I've documented the physics of particle-wall collisions and of particle-particle collisions.  So here I will confine my remarks to atom collisions with the airfoil.  Here I've chosen an airfoil shape that derives from complex numbers called Joukowski airfoil.    

            Since the atoms are flowing (drift speed) rather than the airfoil moving, the wing does not give up energy to the atoms and that means that their collisions with the wing conserve energy.  To conserve energy, the two orthogonal components of the exiting atom's velocity must have the sum of their squares equal to the sum of the squares of the incident velocity components. For a smooth surface, the usual assumption is that the exiting velocity component tangential to the airfoil surface is the same as the incident tangential velocity  component.  That means that the exiting velocity normal to the airfoil has to be opposite to the incident velocity component.  On a very fine spatial scale, no surface is smooth with respect to the de Broglie wavelength of the atoms (approximately 0.05 nanometers for air at room temperature).  However, the assumption above will represent a reasonable average for the behavior of the atoms that hit the airfoil.  

Joukowski Airfoil   

Let Z be the coordinates of the original circle in the complex plane.  Let the radius of this circle be

r= a+b 2 MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadkhacqGH9a qpdaWcaaqaaiaadggacqGHRaWkcaWGIbaabaGaaGOmaaaaaaa@3B63@  

(1.1)

where a and b are the horizontal and vertical semi-axes of an ellipse to which this airfoil will reduce with no x and y offsets for the original circle.

Also define the parameter

c= 1 2 a 2 − b 2 MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadogacqGH9a qpdaWcaaqaaiaaigdaaeaacaaIYaaaamaakaaabaGaamyyamaaCaaa leqabaGaaGOmaaaakiabgkHiTiaadkgadaahaaWcbeqaaiaaikdaaa aabeaaaaa@3E06@  

(1.2)

Let the x and y offset of the center of this circle from z=0 be

z o =δx+iδy MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadQhadaWgaa WcbaGaam4BaaqabaGccqGH9aqpcqaH0oazcaWG4bGaey4kaSIaamyA aiabes7aKjaadMhaaaa@402F@  

(1.3)

Then the airfoil boundary is formed by the expression:

z=Z+ c 2 Z MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadQhacqGH9a qpcaWGAbGaey4kaSYaaSaaaeaacaWGJbWaaWbaaSqabeaacaaIYaaa aaGcbaGaamOwaaaaaaa@3C7B@  

(1.4)

where Z is described parametrically by: 

Z(θ)=a(cosθ+isinθ)− z o MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadQfacaGGOa GaeqiUdeNaaiykaiabg2da9iaadggacaGGOaGaci4yaiaac+gacaGG ZbGaeqiUdeNaey4kaSIaamyAaiGacohacaGGPbGaaiOBaiabeI7aXj aacMcacqGHsislcaGG6bWaaSbaaSqaaiaad+gaaeqaaaaa@4B10@  

(1.5)

                                                                                                                                               

Finding the normal vectors of the airfoil boundary

            We define an array of points, zB, Vs angle θ along the boundary of the airfoil.  Then the tangent vector at each of these points is given by the complex vector:

t i = z i+1 − z i MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadshadaWgaa WcbaGaamyAaaqabaGccqGH9aqpcaWG6bWaaSbaaSqaaiaadMgacqGH RaWkcaaIXaaabeaakiabgkHiTiaadQhadaWgaaWcbaGaamyAaaqaba aaaa@3FD4@  

(1.6)

and the outward normal vector is obtained from the tangent vector by the simple expression

n i =[Im( t i ),−iRe( t i )] MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaad6gadaWgaa WcbaGaamyAaaqabaGccqGH9aqpcaGGBbGaciysaiaac2gacaGGOaGa aiiDamaaBaaaleaacaWGPbaabeaakiaacMcacaGGSaGaeyOeI0Iaai yAaiaackfacaGGLbGaaiikaiaacshadaWgaaWcbaGaamyAaaqabaGc caGGPaGaaiyxaaaa@47BB@  

(1.7)

Determine if a point (or particle) is inside or outside the Joukowski airfoil

            In order to know when a particle collides with the boundary, we need to distinguish whether any part of the particle is inside the boundary.

            When defining the airfoil boundaries in the previous section, we need to save two arrays.  First save an array, zB, of the points of the boundary.  Then use this array to compute an array, n, of the outward normal vectors of the boundary at all the boundary points.  To determine if a point, z, is inside the boundary compute all the magnitudes

s i =|z−z B i | MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadohadaWgaa WcbaGaamyAaaqabaGccqGH9aqpcaGG8bGaamOEaiabgkHiTiaadQha caWGcbWaaSbaaSqaaiaadMgaaeqaaOGaaiiFaaaa@3FE3@  

(1.17)

and find index, ic, of the least magnitude.  This ic will be the closest boundary point to the point z.  Now form a vector that points from the zB[ic] to z.  Then take its dot product with n[ic].  If the dot product is negative, then the point is inside the boundary.  Otherwise it is outside.  This method is simple and fast for all boundaries that are not re-entrant, i.e. for all boundaries that don't form more than  one loop.  The problem with more than one loop lies in the fact that the method for computing the outward normal becomes more complicated for this case.  One would have to build re-entrant recognition into the normal calculating algorithm.

 

 

Using the Normal Vector to Compute the Lift and Drag Contributions at Each Impact

            First we compute the dot product of the momentum vector with nxy.

p n = n xy •p MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadchadaWgaa WcbaGaamOBaaqabaGccqGH9aqpcaWHUbWaaSbaaSqaaiaahIhacaWH 5baabeaakiaahkcicaWHWbaaaa@3E03@  

(1.8)

Then we compute the change in the momentum vector

δp=2 p n n xy MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabes7aKjaahc hacqGH9aqpcaaIYaGaamiCamaaBaaaleaacaWGUbaabeaakiaah6ga daWgaaWcbaGaamiEaiaadMhaaeqaaaaa@3F87@  

(1.9)

The y component of this is the contribution to the lift, L

δL=δp•y MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabes7aKjaadY eacqGH9aqpcqaH0oazcaWHWbGaaCOiGiaahMhaaaa@3DD2@  

(1.10)

and the -x component of it is the contribution to the drag D:

δD=−δp•x MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabes7aKjaads eacqGH9aqpcqGHsislcqaH0oazcaWHWbGaaCOiGiaahIhaaaa@3EB6@  

(1.11)

Comparison of Animation Results with Standard Equations

For 2 dimensional space, the standard equations for lift and drag of a thin symmetrical airfoil at low angle of attack are (see http://www.grc.nasa.gov/WWW/K-12/airplane/incline.html)

L≈ ρ 2 v d 2 (2πα)(2a) D≈ ρ 2 v d 2 (2π α 2 )(2a) MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOabaeqabaGaamitai abgIKi7oaalaaabaGaeqyWdihabaGaaGOmaaaacaWG2bWaa0baaSqa aiaadsgaaeaacaaIYaaaaOGaaiikaiaaikdacqaHapaCcqaHXoqyca GGPaGaaiikaiaaikdacaGGHbGaaiykaaqaaiaadseacqGHijYUdaWc aaqaaiabeg8aYbqaaiaaikdaaaGaamODamaaDaaaleaacaWGKbaaba GaaGOmaaaakiaacIcacaaIYaGaeqiWdaNaeqySde2aaWbaaSqabeaa caaIYaaaaOGaaiykaiaacIcacaaIYaGaamyyaiaacMcaaaaa@577E@  

(1.12)

where vd is the drift speed of the air along the x direction and ρ is the air mass per unit area.  The result of equation (1.12) for the simulation, at, say 10 degrees or 0.16 radians, with 2a=300, vd=2.5, ρ=0.00125  is L=1.29.  The animation result for the same conditions is L=1.65.  Therefore, the lift results for the animation are reasonably in agreement with the standard thin airfoil expressions. 

Conclusions

            Although the animation results in lift and drag numbers that are comparable to real world values, it is clear that some real world experiments that obtain difference in the speed of air flow over the top and bottom of the airfoil disagree with those obtained in the animation.  Thus there must be a more complex interaction at the boundary layer at the surface of the airfoil.  Since there are many real world cases where air viscosity can be neglected, we are left only with the (sub)microscopic roughness of the airfoil to explain how the airfoil re-shapes the contours of constant air velocity on its top and bottom.