Precession of a Rotating Charged Loop

Introduction

A precessing rotating charged loop is a good prelude to understanding the effects of a magnetic field on electrons and nucleons in atoms. The animation that this document describes should give the learner some hands-on experience with that precession,

Figures

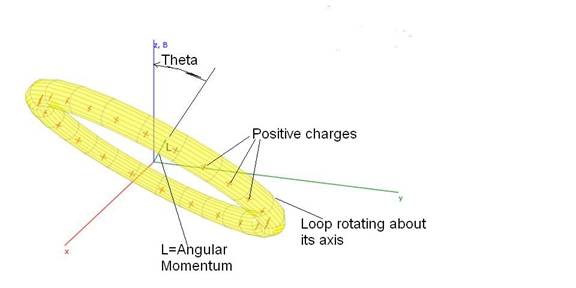
Figure 1: The charged loop precesses about the z axis and B vector at angle q. The diagram shows the instantaneous angular momentum vector, L, as well as the center of mass. The torque on the loop is t=m x B where x indicates the cross product of the magnetic moment vector m with the magnetic field vector B.

Ratio of Magnetic Moment, m, to Angular Momentum L

For a very thin toroid of radius r and mass m:

For a charged toroid of radius r and total charge q:

The ratio is:

Calculations

In steady precession the angular momentum can be described as:

(1)

where the bold x, y and z are unit vectors in the x, y, and z directions, respectively, q is the tilt angle with respect to the z axis and w is the angular rate of precession.

The torque, t, that causes the precession has to be synchronous with L and is:

(2)

And the pertinent equation relating the precession to the torque is:

(3)

From equation 3 we easily obtain the angular rate of precession as:

(4)

Summary

Note that the precession frequency is independent of the angle of tilt because both the torque and dL/dt are proportional to the sine of the tilt angle. If the loop angular speed decreases, however, L₀ decreases, increasing the rate of precession and the tilt will become larger.