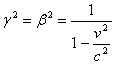Lorentz Transformation from First Principles

The conversion from the Galilean transformation to the relativistic transformation has some mixing of time and space variables.

(1)

where g, b, and a are presently unknown.

We can always invoke the constancy of the speed of light and let x=ct and x’=ct’ and substitute these into equations 1 to get some information on the relationships between g, b, and a.

(1a)

(1b)

The condition that there be no special frame requires that the inverse transform’s only difference is that v->-v (and, as it will turn out, a->-a).

(2)

We cans also solve equations 1 for x and t:

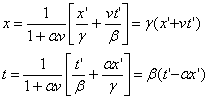(3)

From the first equation, setting the coefficients of x’ equal, we get:

and from the second equation setting the coefficients of t’ equal we get:

From which we conclude that g=b.

Now, using equation 1b we have:

so that

and thus