Lorentz Transformation Derivation by Requiring Self Consistency

The conversion from the Galilean transformation to the relativistic transformation has some mixing of time and space variables.

(1a,b)

where g, b, and a are presently unknown. See Appendix for a derivation of the sign of a.

The reason for the presence of the ax term in equation 1b is that the time must be corrected for the relative speed, v, between the frames of reference.. The time that light takes to travel from x to the origin where x=0 is:

(2)

During the time dt, the frame of reference moves a distance

(3)

Therefore the time correction for this distance is:

(4)

Which means that the term a in equations 1 is, using the result from the Appendix:

(5)

And equations 1a,b become:

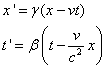(1a,b)

Since all inertial frames of reference have the same physical laws, the conversion from x to x’ has to have the same coefficients except for the difference in sign of v:

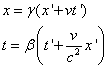(1b)

We can now use equations 1a in equations 1b:

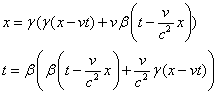(1a,b)

From equations 1a,b we must conclude the following:

or else the equations for x and t would be dependent on both x and t.

Then equations 1a,b become:

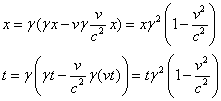(1c,d)

If the equations for x and t are to be self-consistent we must have:

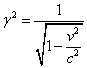
With that stipulation, equations 1c,d become:

Appendix

We can use the following fact to determine the sign of a. In relativity, it is always true that spacetime intervals are conserved thus:

Then equations 1a,b can be rewritten:

(1’a,b)

or combining the two equations:

(1’c)

So since c, g and b always have to be positive, we know that the sign of a is the opposite of the sign of v.