Eddy Current Drag for A Magnet in A Conductive Pipe

Introduction

If you slide a magnet on a sheet of copper (a good conductor) it will slow down much more quickly than when sliding on a sheet of plastic (a poor conductor) even when the surfaces of both sheets have the same coefficient of friction. The reason is that the moving magnet creates large eddy currents due to the change of change of magnetic flux in the copper sheet. The present document concerns itself with a more efficient geometry than a sheet as shown below.

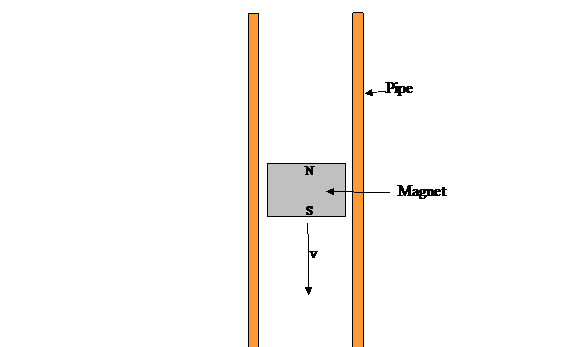
Figure 1: Cylindrical magnet in a vertical copper pipe. When the magnet moves down the pipe, it creates eddy currents that limit its falling speed, v, to a constant value.

What is interesting about this problem is that, because of symmetry, the magnet by itself would not produce magnetic fields due to eddy currents that would resist the force of gravity. However, when the electromotive potential due to the eddy currents adds new eddy currents to those of the falling magnet, the symmetry is broken and a magnetic force that opposes gravity is formed.

Motion of the magnet

The Newton's law differential equation is

$m \frac{d v}{d t} = m g - b v$

(1.1)

where m is the magnet mass, v is the downward speed, g is the acceleration of gravity, and bv is the velocity-dependent drag force due to eddy currents in the pipe.

The solution for this equation is

$v = \frac{m g}{b} [1 - \exp (- \frac{b}{m} t)]$

(1.2)

So that, for reasonably large drag forces, v comes to a steady state value very quickly.

What is the value of b? Experimentally, for a 7 mm diameter copper tube, with 1 mm wall thickness and for approximately 5 mm diameter magnets of 7 mm length and approximately 1 Tesla strength at their poles, the steady state speed v_ss =mg/b is about 60 mm/second. Since mg is about 0.013 Newton, the value of b must be:

$b = m g / v_{s s} = 0.013 / 0.06 = 0.2 N e w t o n - \sec / m e t e r$

(1.3)

Of course this drag coefficient results from the eddy currents induced in the copper pipe by the moving magnet. The power dissipated by these currents while the magnet moves through the earth's gravitational field without speeding up must be:

$P_{d i s} = \frac{d E}{d t} = m g v_{s s}$

(1.4)

and this power has to be

$P = ρ_{c u} \int 2 π r J {(r, z)}^{2} d r d z$

(1.5)

where ρ_cu is the resistivity of copper, J is the current density in the copper, and the integral is over the circumferential cross-section of the copper pipe.

The next important question is how the current density, J, arises. That is due to Lenz's law which states:

$V_{c i r c u m f e r e n t i a l} = - \frac{d Φ_{B}}{d t}$

(1.6)

where

$Φ_{B} (r) = \int_{0}^{r} 2 π r' B (r') d r'$

(1.7)

and it is V_{circumferential} that induces the current density:

$J_{ϕ} (r) = σ_{c u} \frac{Φ_{c i r c u m f e r e n t i a l}}{2 π r}$

(1.8)

Just one more equation is needed since we don't have dΦ_B/dt:

$\frac{d Φ_{B}}{d t} = v_{s s} \frac{d Φ_{b}}{d z}$

(1.9)

Computing the Magnetic field due to Magnet and Pipe Combined

The partial differential equation for the magnetic field is:

$\nabla \times [\frac{(\nabla \times A - P)}{μ}] + J = 0$

(1.10)

where A is the vector potential, P is the polarization (related to magnetization and often called the remanence field), and μ is the permeability. We assume that P is constant in the permanent magnet and solve this equation for A. Then the magnetic induction is:

$B = \nabla \times A$

(1.11)

Since the whole problem is axi-symmetric, we solve it in cylindrical coordinates using finite element methods. A typical result is shown below in Figure 2.

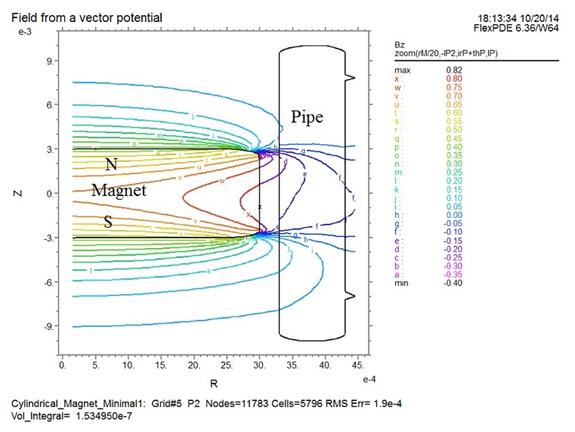
Figure 2: Showing a contour plot of the axial magnetic induction, B_z, due to a magnet of polarixation P=1 Tesla in a copper pipe . The contour lines are skewed vertically because of the eddy currents in the copper pipe.

The opposing field exerted by the eddy currents in the pipe

Since the magnet moves at constant velocity inside the pipe, the opposing force must be the weight of the magnet:

$F_{e d d y c u r r e n t} = m g$

(1.12)

The mass of the magnet is computed by the equation

$m = ρ V = ρ π r_{m}^{2} h_{m}$

(1.13)

where ρ is the density (kg-m^-2) of the magnet material, r_m is the magnet radius and h_m is its height.

A formula for the force provided by the interaction of the magnet field and the eddy current field is:

$F_{e m} = \frac{B_{m} B_{e} A_{m}}{2 μ_{0}}$

(1.14)

where B_m is the permanent magnet's field (about 1 Tesla), B_e is the eddy current field, and A_m is the magnet cross-sectional area. Setting F_em equal to mg provides the equation for B_e.

$B_{e} = \frac{2 μ_{0} m g}{B_{m} A_{m}} = \frac{2 μ_{0} ρ h_{m} g}{B_{m}}$

(1.15)

For our 1 Tesla magnet, B_e turns out to be 3.3x10^-11 Tesla.