Black Body Radiation Law and the Birth of Quantum Mechanics
Introduction
The concept of a quantum of energy was invented in order to explain what was called the “ultraviolet catastrophe” associated with the electromagnetic (EM) radiation that was theoretically expected from small hole in the wall of a heated cavity called a “black body”. What was expected was that there would be an energy kT, where k is Boltzmann’s constant and T is the absolute temperature expressed in degrees Kelvin, associated with each permissible mode of EM radiation of the cavity. But it was shown that the equation for the density of modes as a function of frequency, f, per unit EM frequency increased without limit ( proportional to f2) as the observed frequency, f, increased and, therefore, so would the emitted power.
By introducing the factor
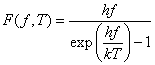 (1)
(1)
instead of the kT which multiplied each mode in the cavity, Max Planck was able to explain the experimental data of measurements of EM radiated power Versus frequency from the black body. The factor h in the exponent in equation 1 is the celebrated “Planck’s constant”, a very small quantity equal to 6.6x10-34 Joule-seconds. Note that, when hf<<kT (the low frequency limit), the factor in equation 1 reduces to kT. Also note that, in the high frequency limit, the exponential factor in the denominator of equation 1 will dominate the f2 factor in the density of modes and thereby avoid the “ultraviolet catastrophe”.
Modes of a Simple Parallelepiped Cavity
For definiteness the cavity we should assume here will have walls that cause the tangential component, Et, of the electric field of the EM wave to be identically zero. For higher mode numbers (or higher frequencies) the results wouldn’t change much if we instead assumed that the Et at the walls was a small (but constant for all wall points) fraction of its peak value within the cavity. As such, the lowest frequency and smallest wave vector, k, that the cavity can support is:
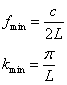 (2)
(2)
where c is the speed of light and L is the width of the cavity (assumed to be a cube at this point). In equation 2 I’ve also assumed that the wave is parallel to one of the edges of the cavity. To be more general, we should express the wave vector as:
![]() (3)
(3)
where x, y, z with the carat above them are unit vectors along the orthogonal edges of the cavity and generically:
![]() (4)
(4)
where
![]() (5)
(5)
so that from equation 4 we have:
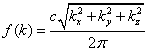 (6)
(6)
Obviously, while still observing the boundary conditions, we can have waves with higher k values than in equation 2 in each of the 3 directions and these are expressed as:
![]() (7)
(7)
where nx, ny, nz are positive integers and Lx, Ly, Lz are the lengths of the edges of the cavity. Then equation 6 becomes:
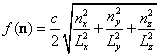 (8)
(8)
It’s obvious that the values of nx, ny, nz where f(n) is nearly constant lie on the surface of a three axis (triaxial) ellipsoid in mode index space of major axes
![]()
Further discussion of
the non-cubic cavity will be referred to Appendix B.
The total number, N, of different n’s that lie in a single octant (where nx, ny, nz are all positive) of a sphere is
![]() (9)
(9)
The number of n’s per unit change of the radius of that spherical surface is
![]() (10)
(10)
This area represents the number of modes (the number of different k directions) per unit n. Now we need to re-write equation 10 in terms of frequency. Solving equation 8 for n we have:
![]() (11)
(11)
and thus the density of modes per unit n in terms of frequency is :
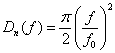 (12)
(12)
where
![]() (13)
(13)
and f0 is the lowest frequency of the cubic cavity.
Equation 13 is correct if we have only one polarization state but we have 2 so that:
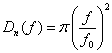 (14)
(14)
Equation 14 is still the density per unit n. To convert it to units of per unit frequency we need to take the differential of equation 11:
![]() (15)
(15)
And then use equation 15 in equation 14 to obtain:
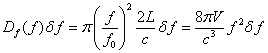 (16)
(16)
where V=L3.
Converting Mode Density to Spectral Power:
We want to compute the power per frequency interval and per solid angle that emerges from a very small (relative to L) diameter hole in the wall of the black body. In the classical case, each of the modes have energy kT associated with them. The energy density per unit frequency per unit volume in the cavity is therefore just the mode density in equation 16, divided by the volume V and multiplied by kT.
![]() (17)
(17)
The waves in the cavity move in all directions so the solid
angle question is handled by dividing by 4p
thus: ![]()
![]() (18)
(18)
where dW is the solid angle increment. The quantity dW corresponds to the area of the detector divided by the square of the distance r of the detector plane from the hole plane when the planes are assumed to be co-parallel.
Further, the energy emerges from the hole at the speed of light so the light energy that passes through a unit area of the hole per second is
![]() (19)
(19)
We see from equation 19 that the “ultraviolet catastrophe” arises from the f2 in the numerator.
In order to explain the experimental results where the actual spectrum drops off approximately exponentially above a certain wavelength, Max Planck in 1900 changed the kT of equation 19 to a quantity hf and also added a denominator which yielded
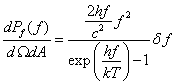 (20)
(20)
Although experimental measurements of spectral power were not too accurate at that time, equation 20 was ultimately proved to be accurate. The quantity h that Planck needed to evaluate in order to fit the spectral data was 6.6x10-34 Joule seconds.
Discussion
The startling conclusion from
equation 20 is that kT was replaced by hf.
It meant that h had to be a brand new physical constant similar in
importance to the gravitational constant, G or the Boltzmann constant, k. It also meant that the energy of a mode of
frequency f could increase only in units of hf independent of the value of kT,
although its probability of increasing was
dependent on kT.
Appendix A
Displaying the Mode k Vectors of the First Octant-Cubic Cavity Case.
We want to show, on the surface of an octant, all the valid k vectors of a rectangular box up to a given index, nI,. These k vectors correspond to a single frequency, f, which has the k value
![]() (A1)
(A1)
where c is the speed of light.
To start we step through all (nx, ny, nz) from zero up to nI and check to see if
![]() (A2)
(A2)
where defect is a decimal number less than 1 which attempts to avoid having any of the sets of the underlying octant included in the display. However, sometimes this doesn’t exclude enough modes and sometimes it is too exclusive.
The reason is that sets of integer triplets which lie on the surface of an octant with maximum value nI cannot correspond to a single k. One component to this is that the square root in equation 1 is generally not an integer. So, unless otherwise devised, there will always be some variability in the total number included on the surface of the octant.
For example, if (nx, ny, nz) range from 0 through nI=20, then we should expect that there would be a total number of modal triplets nT:
![]() (A3)
(A3)
since the radius of the octant is nI
and its area is pnI2/2. We actually obtain 676 triplets using a
defect of 0.5 in equation 1. The extra nI in equation 2 is due to the fact that (nx,
ny, nz) can have zeros for two out of its three values so
that two edges of the ellipsoidal triangle (say the right edge and the bottom
edge) be populated with zeros (for our case, the ny=0 and the nz=0
edges).
An algorithm for getting exactly the nT given in equation 2 can be defined as follows.
- Save all triplets that have a larger defect of 1.0 or less in equation 1. Save their defects as well. This will result in many more triplets than nT. Save a Boolean array that corresponds to the defect array and set all its initial value to true.
- Sort through their defects and find the nT that have the lowest defects.
- Find the highest defect and set its Boolean array value to false as well as reducing the total true count.
- Continue finding the highest defects that are not false and reducing the true count of the Boolean array until count gets to nT.
- Plot the remaining true points.
This algorithm will not result in perfectly uniformly spaced modes on the surface of the octant but we shouldn’t expect that to be the case since the resulting modes will be only approximately those corresponding to k in equation 0.
Appendix B
Displaying the Mode k Vectors of the First Octant-Rectangular Cavity Case.
The surface of the tri-axial ellipsoid in (nx, ny, nz) space is obtained from the
equation:
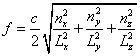 (B1)
(B1)
where the major axes of the tri-axial ellipsoid are
![]() (B2)
(B2)
The area of one octant of this ellipsoid (corresponding to the number of modes on the octant) is given within 1% by the equation[1]:
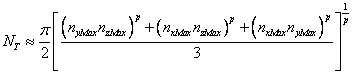 (B3)
(B3)
where p=1.6075. For near-unity ratios of the (Lx, Ly, Lz ) lengths the error in surface area is much lower.
To actually use equation B1 on the computer, we proceed as in Appendix A.
We step each of (nx, ny, nz) from (0,0,0) to (nxMax, nyMax, nzMax). As we do so, we record the defect:
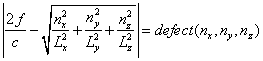
If the defect is less than 1/<L> (where <L> is the average of (Lx, Ly, Lz)), then, in arrays, we save the n vector, the defect value, and also set the Boolean value of an array corresponding to the defect array to true.
After saving all pertinent candidate n vectors, we then go back through the defect list multiple times setting the true Boolean array values corresponding to the largest defects to false until the total number of modes is equal to the number computed in equation B3. The remaining true n vectors are then plotted.
The above operations can be performed again with a value of
f that is larger by c/(2<L>) to plot the modes
that we get increasing the frequency. Of course, we already have the
surface area due to a change in f
by using equations B2 and B3 and we just need to iterate these equations to get
the change in total modes per change in frequency.