2D Molecular Energy Distributions Animation

Introduction

            This animation demonstrates the dependence of 2D molecular energy distributions on vibration mode excitation as well as linear translation and rotation.  The results are interpreted by both histograms of the frequency distributions of energies and algebraic plots of  the expected distributions.

Figures:

 

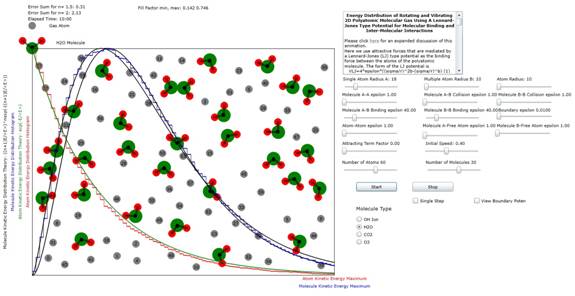
Figure 1:  Plot of atomic and molecular distribution of molecule H2O (water).  The results (n=1.5) indicate that only two of the possible 3 modes of planar vibration  are excited at these energy levels.

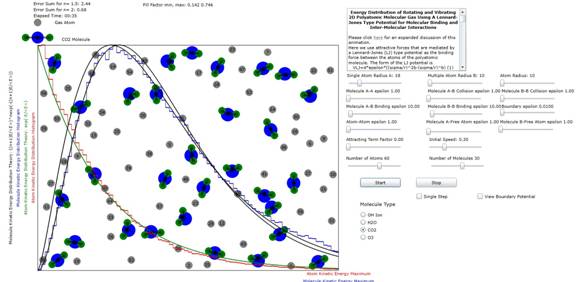
Figure 2:  Plot of atomic and molecular distribution of molecule CO2 (carbon dioxide).  The results (n=2) indicate that all of  the possible 3 modes of planar vibration  are excited at these energy levels.

 

 

 

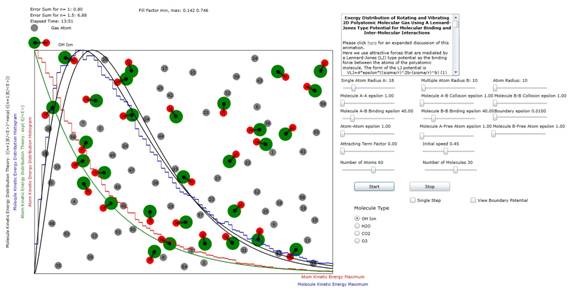
Figure 3:  Plot of atomic and molecular distribution of the OH ion (hydroxide).  The results (n=1) indicate that single  mode of planar vibration  is marginally  excited at these energy levels.

 

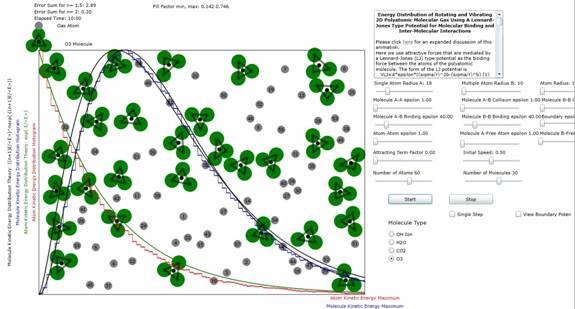
Figure 4:  Plot of atomic and molecular distribution of molecule O3 (ozone).  The results (n=2) indicate that all 3  of the possible 3 modes of planar vibration  are excited at these energy levels.

 

 

Analysis

For each degree of freedom, the multiplier of the fraction in the exponential increases by 1/2 while the power of the multiplier in the expression for energy distribution increases by 1/2.  Then for 2n+2 degrees of freedom, the expression for distribution of energies is

f(T)= ( (n+1)T <T> ) n exp( − (n+1)T <T> ) MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadAgacaGGOa GaaiivaiaacMcacqGH9aqpdaqadaqaamaalaaabaGaaiikaiaad6ga cqGHRaWkcaaIXaGaaiykaiaadsfaaeaacqGH8aapcaWGubGaeyOpa4 daaaGaayjkaiaawMcaamaaCaaaleqabaGaamOBaaaakiGacwgacaGG 4bGaaiiCamaabmaabaGaeyOeI0YaaSaaaeaacaGGOaGaamOBaiabgU caRiaaigdacaGGPaGaamivaaqaaiabgYda8iaadsfacqGH+aGpaaaa caGLOaGaayzkaaaaaa@517F@  

(1.1)

where T is the total kinetic energy of the molecule.

If we want to convert this to a probability we must set the integral from 0 to infinity of f(E) to 1:

 

P(T)= ( (n+1)T <T> ) n exp( − (n+1)T <T> ) ∫ 0 ∞ ( (n+1)T <T> ) n exp( − (n+1)T <T> )dT MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOabaeqabaGaamiuai aacIcacaWGubGaaiykaiabg2da9maalaaabaWaaeWaaeaadaWcaaqa aiaacIcacaWGUbGaey4kaSIaaGymaiaacMcacaWGubaabaGaeyipaW Jaamivaiabg6da+aaaaiaawIcacaGLPaaadaahaaWcbeqaaiaad6ga aaGcciGGLbGaaiiEaiaacchadaqadaqaaiabgkHiTmaalaaabaGaai ikaiaad6gacqGHRaWkcaaIXaGaaiykaiaadsfaaeaacqGH8aapcaWG ubGaeyOpa4daaaGaayjkaiaawMcaaaqaamaapehabaWaaeWaaeaada WcaaqaaiaacIcacaWGUbGaey4kaSIaaGymaiaacMcacaWGubaabaGa eyipaWJaamivaiabg6da+aaaaiaawIcacaGLPaaadaahaaWcbeqaai aad6gaaaGcciGGLbGaaiiEaiaacchadaqadaqaaiabgkHiTmaalaaa baGaaiikaiaac6gacqGHRaWkcaaIXaGaaiykaiaadsfaaeaacqGH8a apcaWGubGaeyOpa4daaaGaayjkaiaawMcaaiaadsgacaWGubaaleaa caaIWaaabaGaeyOhIukaniabgUIiYdaaaaGcbaaaaaa@6F52@  

(1.2)

The integral in the denominator is fairly simple letting u= (n+1)T <T> MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadwhacqGH9a qpdaWcaaqaaiaacIcacaWGUbGaey4kaSIaaGymaiaacMcacaWGubaa baGaeyipaWJaamivaiabg6da+aaaaaa@3FA3@  :

∫ 0 ∞ u n exp[−u]du= Γ(n+1) MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaamaapehabaGaam yDamaaCaaaleqabaGaamOBaaaakiGacwgacaGG4bGaaiiCaiaacUfa cqGHsislcaWG1bGaaiyxaiaadsgacaWG1bGaeyypa0daleaacaaIWa aabaGaeyOhIukaniabgUIiYdGccqqHtoWrcaGGOaGaamOBaiabgUca RiaaigdacaGGPaaaaa@4B69@  

(1.3)

and therefore

∫ 0 ∞ ( (n+1)T <T> ) n exp( − (n+1)T <T> )dT =Γ(n+1) <T> n+1 MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaamaapehabaWaae WaaeaadaWcaaqaaiaacIcacaWGUbGaey4kaSIaaGymaiaacMcacaWG ubaabaGaeyipaWJaamivaiabg6da+aaaaiaawIcacaGLPaaadaahaa Wcbeqaaiaad6gaaaGcciGGLbGaaiiEaiaacchadaqadaqaaiabgkHi TmaalaaabaGaaiikaiaad6gacqGHRaWkcaaIXaGaaiykaiaadsfaae aacqGH8aapcaWGubGaeyOpa4daaaGaayjkaiaawMcaaiaadsgacaWG ubaaleaacaaIWaaabaGaeyOhIukaniabgUIiYdGccqGH9aqpcqqHto WrcaGGOaGaamOBaiabgUcaRiaaigdacaGGPaWaaSaaaeaacqGH8aap caWGubGaeyOpa4dabaGaamOBaiabgUcaRiaaigdaaaaaaa@5F99@  

(1.4)

P(T)= (n+1) ( (n+1)T <T> ) n exp( T <T> n+1 ) Γ(n+1)<T> MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadcfacaGGOa GaamivaiaacMcacqGH9aqpdaWcaaqaaiaacIcacaWGUbGaey4kaSIa aGymaiaacMcadaqadaqaamaalaaabaGaaiikaiaad6gacqGHRaWkca aIXaGaaiykaiaadsfaaeaacqGH8aapcaWGubGaeyOpa4daaaGaayjk aiaawMcaamaaCaaaleqabaGaamOBaaaakiGacwgacaGG4bGaaiiCam aabmaabaWaaSaaaeaacaWGubaabaWaaSaaaeaacqGH8aapcaWGubGa eyOpa4dabaGaamOBaiabgUcaRiaaigdaaaaaaaGaayjkaiaawMcaaa qaaiabfo5ahjaacIcacaWGUbGaey4kaSIaaGymaiaacMcacqGH8aap caGGubGaeyOpa4daaaaa@5B62@  

(1.5)