Animation of a Monochromator
Introduction
A monochromator is a staple of the physics laboratory. With a single compact instrument with one can convert a broad spectrum of light wavelengths into a very narrow range of wavelengths. And the center of this wavelength range can be changed just by rotating a diffraction grating. Its animation provides some good working examples of how light can be manipulated.
Figures
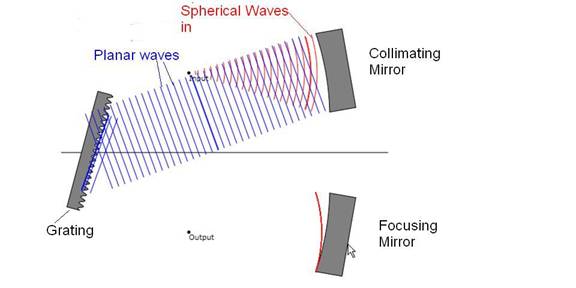
Figure 1: Schematic of the monochromator. The input point and the output points are
clearly shown. The function of the top
mirror is to collimate the spherical (red) incident waves from the input point
so that the waves become planar (blue).
The bottom planar waves that will be accepted through the output hole
are symmetrical with the upper planar waves as will be clear on Figure 2.
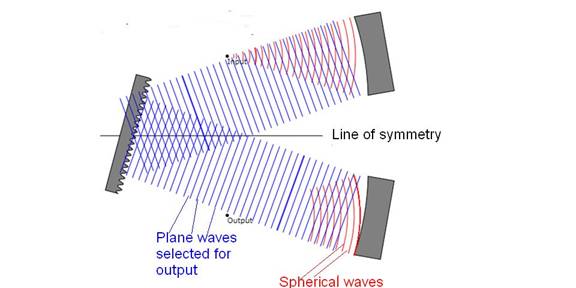
Figure 2: Schematic of the monochromator The function of the bottom mirror is
to converge the planar waves(blue)
incident on it so they become spherical (red) and converge to the output
point.. These converged waves pass through a small hole and fall onto a
detector where the power at the wavelength is measured.
Diffraction
The functions of the top and bottom concave mirrors are to collimate the light and focus a narrow range of wavelengths to the output point as shown in Figures 1 and 2. The light incident on the grating must be collimated (i.e. have planar wavefronts) in order of the grating to provide the same diffraction phase shifts across its entire width. The equation for diffraction of light that is normally incident on a grating is
![]() (1)
(1)
where l is the wavelength being diffracted, m is an integer called the diffraction order (usually m=1), d is the transverse distance between grating rulings, and q is the angle of diffraction. (The rulings (corrugations) shown in Figures 1 and 2 could not be made to scale because the wavelengths of visible light are so short).
The angles of incidence and diffraction of the light for our monochromator are a function of the tilt angle, qG of the grating and the angle of the collimated wavetrain with respect to the Line of Symmetry shown in Figure 2. The latter angle is just twice the mirror tilt angle or 2qM .
![]() (2)
(2)
where the tilt of the grating is measured clockwise from vertical. The diffraction equation for non-normal incidence is:
![]() (3)
(3)
Substituting equation 2 into equation 3 and using some trigonometric identities we get:
![]() (4)
(4)
Discussion
A remarkable difference between the grating monochromator
and that for a prism spectroscope is that here longer wavelengths are obtained
with larger grating tilt angles. Also,
it is impossible to vary the output wavelength of a prism instrument without
simultaneously moving both the light source and the detector.