Equations for reflection at a moving planar interface
Assume a wave from a source in vacuum of the form:
![]()
where ![]() where q is the angle of the light wave propagation with
respect to the x axis and
where q is the angle of the light wave propagation with
respect to the x axis and
![]()
c is the speed of the wave fronts and w is their radian frequency.
Now consider that the interface is moving at a rate v=bc away from the light source along the x direction. Then, using the simple scalar transformations of special relativity, with the primed quantity being that in the moving interface frame of reference we have the following equations.
Source frame: Moving frame:
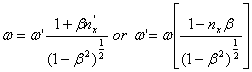 (1)
(1)
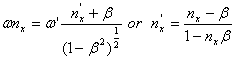 (2)
(2)
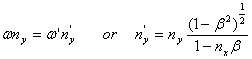 (3)
(3)
Using left sides of equations 1, 2, and 3 but with nx’ negative, we transform w, nx and ny back to the frame of the light source and renaming these with double primed notation:
![]()
Therefore the angle of reflection, q’’, will be given by
![]()
The ratio of the wavelengths of the reflected wave to the incident wave will be the inverse of the frequency ratio:
![]() Recall that the wave fronts
are always observed, from both the source frame and the moving interface frame,
to travel at the speed of light.[1]
Recall that the wave fronts
are always observed, from both the source frame and the moving interface frame,
to travel at the speed of light.[1]