Oscillating Capacitor Slab

Introduction

The electric polarization of a material is important in many applications with the most well-known being a capacitor. In this animation and this document, we explore the polarization phenomenon from the induced electric field energy standpoint. We contrive a composite slab of dielectric that will tend to oscillate between the parallel plates of a simple capacitor because of the increase of dielectric constant (permittivity) with respect to distance from the horizontal center of the slab.

Figures

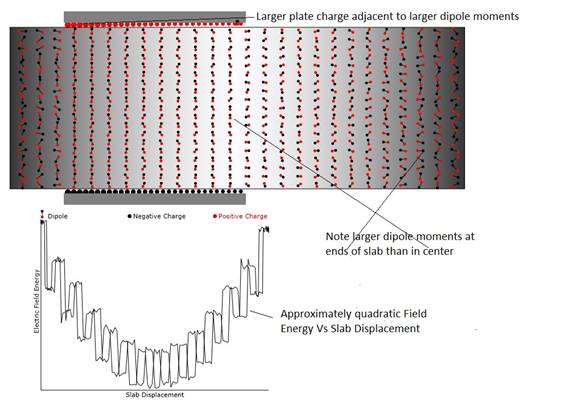
Figure 1:Showing the details of the animation. Please read the embedded notes. Also note that the orientation of the dipoles enveloped by the capacitor plates is more along the electric field direction while, outside the plates, the orientation is random.

Relation between Polarization and Dipole Moments

The electric polarization of a material is the result of the electric field's either inducing dipole moments from atoms or molecules or reorienting the dipole moments of either ionic or covalently bonded molecules so that, on average, they become better aligned with the applied electric field. Since it is easier to visualize the latter, that is model that will be used in this animation. The dipole moment is made up of two separated charges of opposite sign and is defined mathematically as:

where q is the charge at the two ends of vector, d, and m is a vector that points in the direction from the negative (shown as black) to the positive charge (shown as red).

When an electric field is applied to the dipole it creates a torque that tends to align the dipole with the field

so that the dipole and field end up pointing in the same direction. However, the dipoles of the type we are considering are continuously undergoing thermally induced rotation, so that the alignment is never perfect. But since the torque is proportional to the product of the dipole moment and the electric field, the average alignment becomes better as either of these two entities increase. Note that, for the same charge values q, the dipole moment (and the torque) becomes larger when the length of d is increased. That is natural since, for longer d, the leverage that the electric field applies is larger and alignment is greater.

The polarizability of the medium is proportional to the number of dipoles per unit volume times their average dipole moment. The dipole moment per unit volume, p, that is induced by an electric field is:

where obviously aE is the product of the density of dipoles, n_m, times their average moment and times the component of the m that points along E.

where q_Em is the angle between E and m.

A more usual way of expressing the polarization is to write:

where e is the permittivity of the medium and e₀ is the permittivity of vacuum. Note, from the equation for capacitance of a parallel plate capacitor

where Q is the capacitor charge, V the voltage, A the area of the plates, and d is the separation of the plates

that the units of e are Coulombs Volt^-1 meter^-1. Also note that Electric field, E, has units Volts meter^-1. Then the units of P are Coulombs meter^-1 which are the same as the units of p=aE. So P is really synonymous with p and is the dipole moment per unit volume.

Capacitor Energy

For a simple variable dielectric constant slab the capacitance is

where x is the displacement of the slab with respect to its centered position and w is the width of the slab.

The energy with the voltage, V, applied to the capacitor is

The force on the slab is -dU/dx:

which would indicate a force in the +x direction when e>e₀ and x>0. This is just a confirmation that the slab tends to go to the lowest energy state which means that it would be ejected from the plates. We can invert this situation if we had 2 connected slabs with a gap along the x direction between them.

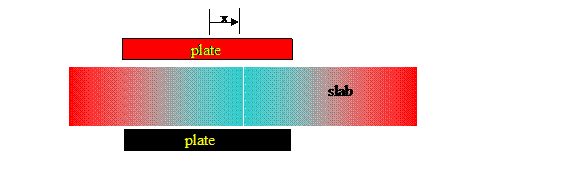
If we desire to have an oscillating slab, we instead assume that the permittivity varies proportionally to x². In the frame of reference of the capacitor slab where x_s=0 at the center of the slab we assume

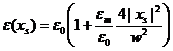
Understanding the Origin of Electric Field Energy Density

The force on the capacitor slab depends on the derivative of the electric energy density. We've learned at our earliest physics classes that the electric energy density is given by

but I'd like to show where this energy comes from when charging a simple parallel plate capacitor.

I will start from the simplest assumption, that force between small charged particles is inversely proportional to the square of their distance of separation, and show that the energy needed to increase the total charge on a capacitor plate by a small amount, q, corresponds to the change of electric field energy in the capacitor. The energy needed to add q to the plate is, of course, provided by the power (voltage) source to which the capacitor is connected.

The y component of the force between q and a small fraction of the surface charge density, s, already on the plate is given by the expression:

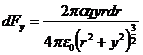
where 2psrdr is the charge in a ring, of width dr, of surface charge centered under the charge q to be added.

To obtain the total force we must integrate over r. We first note that the differential

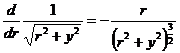
and therefore we can conclude that for a single capacitor plate.

However, since we have 2 oppositely charged capacitor plates we must double F_y and then we have:

The energy required to move q from one capacitor plate to the other is then:

where d is the separation of the capacitor plates. The change in average surface charge density on the plates due to adding q is:

where A is the surface area of the plate. Then we can write that

and then we can integrate both sides over U and s to obtain:

We recognize that the quantity Ae₀/d is the capacitance, C, and therefore we can rewrite:

which is the standard expression for the total energy stored in a capacitor. The energy density in the capacitor is obviously

Further we know that the electric field in a parallel plate capacitor is given by

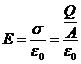
And the energy density in terms of the electric field is given by:

in agreement with the expression we obtained by integrating the energy needed to assemble the charges on the capacitor plates.

So this gives from first principles (at least for the simple case of a parallel plate capacitor) a derivation of the origin of electric energy density expression that we always use.