Parallel Resistors
Introduction
This
animation shows the behavior of charge carriers that contribute to the current
in two parallel resistors. It takes into
account their collisions with the background lattice of the medium which
provides the impedance to charge flow.
It assumes both the carriers and the background lattice (scatterers)
have thermal motion, the former being random translation throughout the
resistor and the latter being simple harmonic motion about the nominal position
of the nucleus in the lattice.
Figures
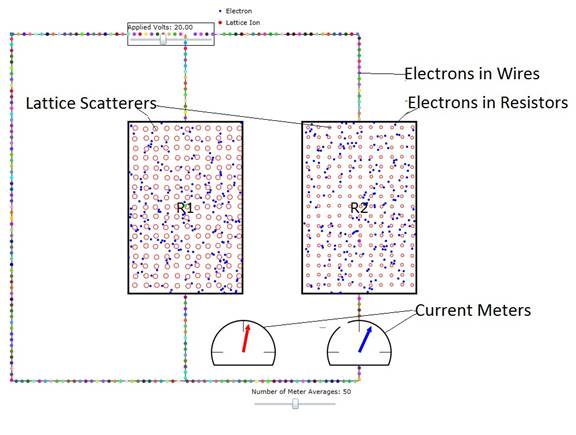
Figure 1: Snapshot of the animation labeling
scatterers, electrons, and current meters.
The rate of electron flow in the left (supply) side of the circuit is
the sum of the rates of the electron flows in the two resistor wires.
Voltage Drop
The current must equal the Voltage drop, V, divided by the
resistance, R. The current is also
defined as the product of the carrier particle charge, e, times the carrier
density n and the drift speed, vd,
times the cross-sectional area of the resistor, A.
The drift speed is the only quantity that requires more
physics explanation. The equation for
drift speed is
where E is the electric field, E=V/L, V is the applied
voltage, L is the length of the resistor, m is the carrier mass, script l is
the mean free path between carrier scatterings and vthermal is
average the thermal speed of the carriers.
An equation for script l is the following:
where nsc is the density of carrier scatterers (often much greater than the density of
carriers themselves) and σ is the combined scatterer-carrier scattering
cross section which has units of length squared. It's important to note that the probability
of electrons scattering from other electrons is much lower than the probability
of electrons scattering from the background lattice. We see that vd, and therefore I,
is inversely proportional to nsc.
where Nsc is the total number of scatterers in
the resistor.
Therefore we can write the current as:
where Nc is the total number of electrons in the
resistor. It can be seen from this equation that the resistance, R, is
Sliders are provided for the user to adjust both Nsc
and Nc.
Thermal Noise Current
Due to the
random thermal motion of the charge carriers, some noise current is generated
even when there is no applied voltage.
This current is computed from the number of carriers hitting the top and
bottom of the resistor per time increment.
The root mean square of the noise current is expected to be:
where N is the total number of carriers in the resistor and
L is its length. If vth=1
length increment per time increment and numerically N=L=300, then we expect the
thermal noise to be one charge per time increment. This is approximately realized in the
program.
The mean value of the thermal speed can be expressed in
terms of temperature:
How the Program Works
The initial
positions of the charge carriers are chosen randomly inside the resistor's
rectangular outline. The initial positions of the lattice nuclei are chosen to
be in a square lattice inside the resistor's rectangular outline. The initial phases of the motion of the
lattice nuclei are also chosen randomly.
The amplitudes of the nuclei simple harmonic motion are set to be
uniform but the directions of this motion are chosen to be random. The initial thermal velocities of the carriers
are set to be between 0 and a user-chosen maximum.
The carrier is accelerated by the electric field provided by
the source voltage. The acceleration
continues unabated until the carrier collides with a scattering nucleus. During
the acceleration it is important to make the product of the program's time
increment, δt, and thermal speed considerably less
than the expected distance between scatterings.
Otherwise the electrons would just blow right past the
scatterers without being impeded by them.
It is also important to keep that same product much less
than the length L of the resistor which is usually a less restrictive condition
than the previous one since A/(Nσ) is generally much less than 1.
At the point of scatter the carrier has reached some
reasonable fraction of its drift velocity (as discussed in the previous
section) but most of this speed is lost (in fact it is negated part of the
time) when the carrier is backscattered by the nucleus. For simplicity, the program assumes that the
drift speed becomes zero at this point. Then the acceleration process is
repeated. As a result of the drift speed,
the carrier makes progress toward the output end of the resistor.
Summary
The
animation is a reasonably valid simulation of charge flow in conductors where
the carriers have both thermal motion and a voltage-induced drift
velocity. The thermal motion of carriers
gives rise to thermal noise (often called Johnson noise) that is seen as the
fluctuations of the two current meters.
The learner may study both the average current and the thermal noise as
a function of thermal speed, voltages, carrier density, scatterer density, and
carrier-scatterer collision cross section.
